A FIGURA EX 2.6 mostra o gráfico da posição de uma partícula.
- Desenhe o gráfico da velocidade da partícula para o intervalo .
- O movimento da partícula possui um ou mais pontos de retorno? Em caso afirmativo, em que instante ou instantes?
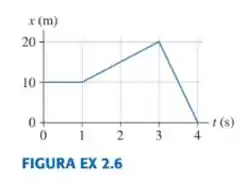
Passo 1
- Desenhe o gráfico da velocidade da partícula para o intervalo .
- O movimento da partícula possui um ou mais pontos de retorno? Em caso afirmativo, em que instante ou instantes?
Bom, temos o gráfico da posição versus tempo e queremos montar um gráfico de velocidade versus tempo.
Para isso precisamos a partir do gráfico que temos, achar a velocidade. Então, vamos lembrar de algo muito importante:
EM UM GRÁFICO DE POSIÇÃO VERSUS TEMPO A VELOCIDADE É IGUAL A INCLINAÇÃO DA RETA
O que vamos fazer é calcular a inclinação da reta para cada uma das retas que aparecem no gráfico e assim descobriremos a velocidade em cada intervalo de tempo e com isso conseguimos montar o gráfico, beleza?
Passo 2
A inclinação de uma reta () é calculada da seguinte maneira:
Em um gráfico de posição versus tempo, o nosso é a posição, o é o tempo e a inclinação da reta é a velocidade, então temos que:
Iremos aplicar essa fórmula para cada reta que aparece no gráfico, beleza?
Passo 3
Para o intervalo teremos:
Para o intervalo teremos:
Para o intervalo teremos:
Passo 4
Agora, com os valores obtidos para a velocidade em cada intervalo de tempo vamos construir o gráfico:
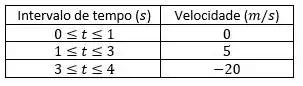
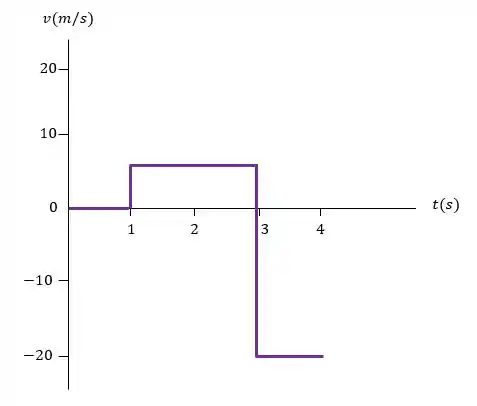
Passo 5
Dizemos que temos um ponto de retorno quando a velocidade muda de sinal, porque isso significa que a partícula estava andando em um sentido e passa a andar no outro sentido.

Então, temos apenas um ponto de retorno, em quando a partícula passa de uma velocidade para .
Resposta
-
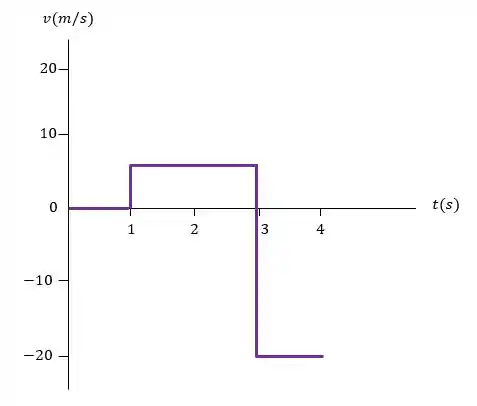
- Há somente um ponto de retorno, em