Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.3 - Ex. 35
Três massas idênticas de são penduradas por três molas idênticas (Figura ). Cada mola tem uma constante de força de e tinha de extensão antes que qualquer massa estivesse presa a ela. (a) Desenhe um diagrama de corpo livre de cada massa. (b) Qual é a distância de cada mola quando pendurada conforme mostrado? (Dica: primeiro isole apenas a massa inferior. Depois, trate as duas massas inferiores como um sistema. Por fim, trate todas as três massas como um sistema.)
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente esboçar o diagrama de corpo livre de cada massa e determinar a distância de cada mola quando pendurada.
Nós sabemos que as três massas têm e cada mola tem uma constante elástica , com comprimento inicial de , antes das massas estarem presas a elas.
Então, vamos esboçar nosso diagrama considerando que todas as molas estarão esticadas, de modo que as forças restauradoras tentaram fazer com que elas voltem para a posição de equilíbrio, “atraindo” as massas.
Depois, vamos considerar que todos os blocos estão em equilíbrio, verificar as forças atuantes em cada uma e determinar a distância pedida.
Vamos lá!
Passo 2
A seguir vamos desenhar as forças agindo em cada corpo:
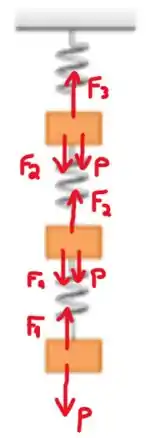
Como todos os blocos estão em equilíbrio, temos que
Com isso, temos que
Passo 3
Usando , podemos escrever:
Substituindo os valores:
Transformando a unidade para centímetros:
Logo,
E
Para achar o tamanho da mola, basta somar o comprimento inicial com o deslocamento calculado. Assim, temos:
Da mesma forma, para a segunda mola:
E para a terceira mola:
Valeu, galera! Até a próxima! 😉