Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.7 - Ex. 67
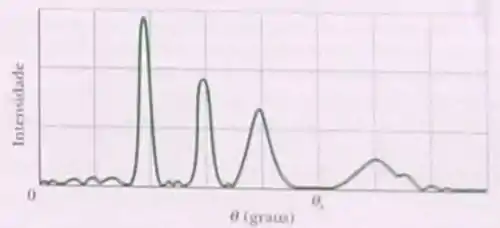
A figura mostra um gráfico de intensidade em função da posição angular para a difração de um feixe de raios por um cristal. A escala do eixo horizontal é definida por . O feixe contém dois comprimentos de onda e a distância entre os planos refletores é . Determine (a) o menor e (b) o maior comprimento de onda do feixe.
Passo 1
(a) Vamos lembrar da expressão matemática da Lei de Bragg:
Essa equação diz que os menores comprimentos de onda vão gerar picos nos menores ângulos. Então nosso menor comprimento de onda está associado ao primeiro pico do gráfico, em .
Já que , e temos cinco “quadrados” no eixo até o , cada “quadrado” vale .
Isso quer dizer que o primeiro pico está aproximadamente em . Vamos substituir isso na nossa fórmula, junto com os outros valores:
Passo 2
(b) Como o feixe tem dois comprimentos de onda, o segundo pico deve estar associado ao outro comprimento de onda (o maior), também em .
Já os outros picos correspondem às outras ordens dos mesmos comprimentos de onda.
Olhando a escala, podemos estimar que o segundo pico está em , então:
Resposta
(a) O menor comprimento de onda é .
(b) O maior comprimento de onda é .