Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.7 - Ex. 73
Considere uma estrutra cristalina bidimensional quadrada, como, por exemplo, um dos lados da estrutura que aparece na figura. A maior distância interplanar dos planos refletores é , a dimensão da célula unitária. Calcule e mostre em um desenho (a) a segunda maior, (b) a terceira maior, (c) a quarta maior, (d) a quinta maior e (e) a sexta maior distância interplanar. (f) Mostre que os resultados dos itens (a) e (e) estão de acordo com a fórmula geral
Onde e são números primos em comum (isto é, que não possuem fatores em comum além da unidade).
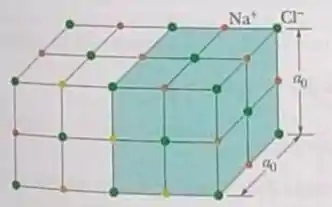
Passo 1
A menor distância interplanar já está demonstada na figura. Agora vamos fazer um desenho bidimensional de um dos lados da estrutura da figura para encontrar as outras.
(a) Para encontrar a segunda maior distância, vamos fazer linhas diagonais, como nesse desenho:
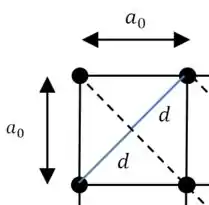
E então podemos usar o teorema de Pitágoras para calcular a distância interplanar :
Beleza, agora vamos usar esse mesmo procedimento para calcular as próximas distâncias.
Passo 2
(b) Para encontrar a terceira maior distância, vamos fazer linhas um pouco mais “inclinadas” para definir os planos:
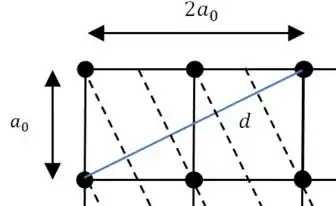
E aplicando o teorema de pitágoras:
Passo 3
(c) Agora vamos desenhar linhas ainda mais inclinadas:
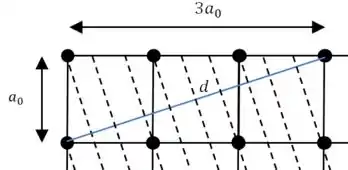
Passo 4
(d) Mais uma vez:
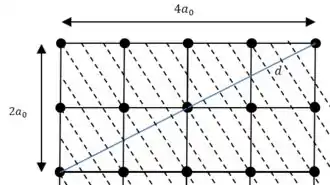
Aproximando :
Passo 5
(e) E por último:
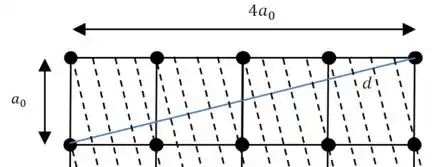
Passo 6
Agora queremos mostrar que os nossos últimos cinco resultados se encaixam nessa fórmula:
Só o que precisamos fazer é achar pares de números “primos em comum” e para cada um dos resultados que achamos. Vamos fazer isso em uma tabela:
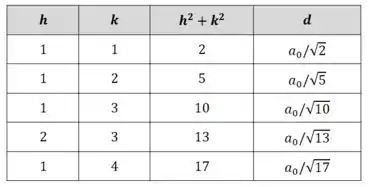
Não esqueça, para que e sejam “primos em comum”, o único divisor comum entre eles tem que ser o número .
Na tabela fica claro que os resultados realmente estão de acordo com a fórmula geral.
Resposta
(a) .
(b) .
(c) .
(d) .
(e) .
(f) Ver tabela.