Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.7 - Ex. 71
Na figura, um feixe de raios X com um comprimento de onda de incide em um cirstal de NaCl fazendo um ângulo de com a face superior do cristal e com uma famíia de planos refletores. O espaçamento entre os planos refletores é . O cristal é girado de um ângulo em torno de um eixo perpendicular ao plano do papel até que os planos refletores produzam máximos de difração. Determine (a) o menor e (b) o maior valor de se o cristal for girado no sentido horário e (c) o maior e (d) o menor valor de se o cristal for girado no sentido anti-horário.
Passo 1
Vamos lembrar da expressão matemática da Lei de Bragg:
Podemos isolar o ângulo de incidência:
Vamos calcular esse ângulo para os primeiros valores de :
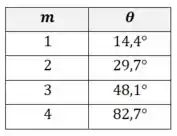
Quando ou , o ângulo de incidência é menor do que , o que indica que o plano está sendo rotacionado no sentido horário.
Quando ou , o ângulo é maior do que , o que indica que o plano está sendo rotacionado no sentido anti-horário.
Para ou mais já não conseguimos calcular o valor do ângulo (já que ).
Passo 2
(a) Pela nossa tabela, dá pra ver que o caso em que o ângulo de incidência diminui menos é quando .
Já que o ângulo foi de para , isso quer dizer que o cristal foi girado em:
(b) Pela mesma lógica, o maior deslocamento do ângulo no sentido horário acontece quando .
Nesse caso o ângulo vai de até , ou seja, o deslocamento total foi:
Passo 3
(c) Pela tabela do passo 1, também dá pra ver que a menor rotação no sentido anti-horário acontece para .
Nesse caso, o ângulo vai de para , então:
(d) E por último, no caso em que o ângulo vai de para , então:
Resposta
(a) .
(b) .
(c) .
(d) .