Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 40

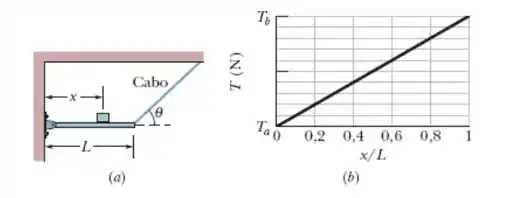
A Figura mostra uma viga horizontal homogênea, de massa m b     e comprimento L , que é sustentada à esquerda por uma dobradiça presa a uma parede e à direita por um cabo que faz um ângulo θ com a horizontal. Um pacote, de massa m p , está posicionado na viga a uma distância x da extremidade esquerda. A massa total é m b   +   m p   =   61,22   k g . A figura mostra a tração T do cabo em função da posição do pacote, dada como uma fração x / L do comprimento da viga. A escala do eixo das tensões é definida por T a   =   500   N   e   T b   =   700   N . Calcule (a) o ângulo θ , (b) a massa m b e (c) a massa m p .

Passo 1

Do equilíbiro de torques com relação à dobradiça, temos:

T L s e n θ - m p g x - m b g L 2 = 0

T = m p g x L s e n θ + m b g 1 2 s e n θ

Analisando essa equação como se fosse a equação de uma reta em x / L , podemos perceber o seu coeficiente angular como sendo igual a m p g s e n θ e o ponto onde ela cruza o eixo das ordenadas igual a m b g 2 s e n θ = 500 N

Passo 2

Analisando o gráfico em b), podemos perceber o coeficiente angular da reta como sendo igual a 700 N - 500 N 1 . Igualando-o ao encontrado no passo 1, vem: 700 N - 500 N 1 = m p g s e n θ = 200 N .

Além disso, temos que m b   +   m p   =   61,22   k g . Então, 1000 s e n ( θ ) / g + 200 s e n ( θ ) / g

Logo, s e n θ ≅ 0,5 e θ = 30 ° .

Passo 3

(b)De posse do θ = 30 ° , temos que m p g s e n θ = 200 N e então m p = 51   k g

Passo 4

(c)Do mesmo modo para m b , temos que θ = 30 ° e m b g 2 s e n θ = 500 N . Então, m b = 10,2   k g

Resposta

  1. 30 °
  2. 10,2   k g
  3. 51   k g
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura, suponha que o comprimento L da barra uniforme seja 3,00m e seu peso seja 200N . Suponha ainda que o bloco tenha um peso P=300N e que θ=30,0 ° . O fio pode suportar uma tensão máxima de 500N
Na figura, uma barra não homogênea está suspensa em repouso, na horizontal, por duas cordas de massa desprezível. Uma corda faz um ângulo θ = 36,9 ° com a vertical; a outra faz um ângulo ϕ = 53,1 ° co
Na figura, um cartaz quadrado homogêneo de 50,0k g , de lado L = 2,00 m , está pendurado em uma barra horizontal de comprimento d h = 3,00 m e massa desprezível. Um cabo está preso emm uma extremidade
Na figura, uma barra fina A B de peso desprezível e comprimento L está presa a uma parede vertical poe uma dobradiça no ponto A e é sustentada no ponto B por um fio fino B C que faz um ângulo θ com a
A figura mostra uma viga vertical homogênea de comprimento L que está presa a uma dobradiça na extremidade inferior. Uma força horizontal F a é aplicada à viga a uma distância y da extremidade inferio