Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 33
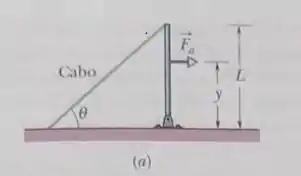
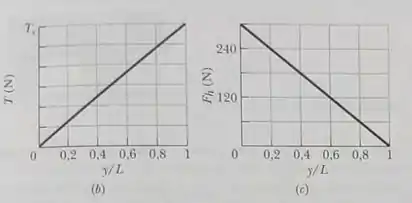
A figura mostra uma viga vertical homogênea de comprimento que está presa a uma dobradiça na extremidade inferior. Uma força horizontal é aplicada à viga a uma distância da extremidade inferior. A viga permanece na vertical porque há um cabo preso na extremidade superior, fazendo um ângulo com a horizontal. A figura mostra a tensão do cabo em função do ponto de aplicação da força, dada como uma fração do comprimento da barra. A escala do eixo vertical é definida por . A figura mostra o módulo da componente horizontal da força que a dobradiça exerce sobre a viga , também em função de Calcule (a) o ângulo e (b)o módulo de .
Passo 1
(a)Considerando o equilíbrio de torques com relação à dobradiça, temos:
Podemos perceber que essa expressão nos mostra que Podemos interpretar isso de forma que é a inclinação do gráfico da tensão em função de dado no enunciado.
Passo 2
Agora, vamos olhar para . A resultante horizontal de forças é dada por
Usando a expressão do passo 1, temos:
Outra coisa legal podemos ver aqui: isso sugere pra gente que a inclinação da reta do gráfico de x é dada por . Observando esse gráfico, podemos calcular essa inclinação. Fazendo isso, encontramos que ela é igual a Então, disso a gente pode concluir que .
Passo 3
Sendo a inclinação do gráfico da figura (por sua vez igual a ), temos que
Como conforme a gente encontrou instantes atrás, temos:
Então:
Passo 4
(b) Conforma e gente sabiamente já encontrou anteriormente, . Legal, né?
Resposta
(a)
(b)