Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 34
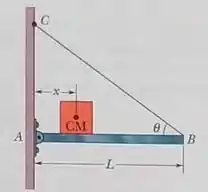
Na figura, uma barra fina de peso desprezível e comprimento está presa a uma parede vertical poe uma dobradiça no ponto e é sustentada no ponto por um fio fino que faz um ângulo com a horizontal. Um bloco de peso pode ser deslocado para qualquer posição ao longo da barra; sua posição é definida pela distância da parede ao seu centro de massa. Determine, em função de , (a) a tensão do fio e as compontentes (b) horizontal e (e) vertical
da força que a dobradiça exerce sobre a barra no ponto .
Passo 1
- Assim como na questão 28, vamos olhar para as forças exercidas sobre a viga:
- Do equilíbrio horizontal das forças que atuam na viga, a gente tem:
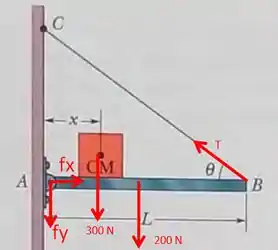
Nesse caso, vamos desprezar o peso da viga (indicado como igual a na figura), pois assim determina o enunciado!
Do equilíbrio de torques com relação à dobradiça, vem:
Então:
sendo o peso do bloco.
Passo 2
Passo 2
(c)Do equilíbrio vertical das forças sobre a viga, finalmente, temos:
Resposta
(a)
(b)