Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 30
Na figura, um cartaz quadrado homogêneo de , de lado , está pendurado em uma barra horizontal de comprimento e massa desprezível. Um cabo está preso emm uma extremidade da barra e em um ponto de uma parede a uma distância acima do ponto onde a outra extremidade da bata está presa na parede por uma dobradiça. (a)Qual é a tensão do cabo? Qual é (b) o módulo e (c) o sentido (para a esquerda ou para a direita) da componente horizontal da força que a dobradiça exerce sobre a haste e (d) o módulo e (e) o sentido (para cima ou para baixo) da componente vertical dessa força?
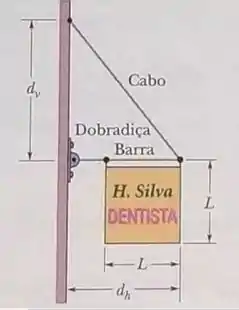
Passo 1
(a)O primeiro e mais importante passo, como já vimos, é esquematizar no desenho as forças que atuam sobre o cartaz e sobre a haste, assim como demonstramos na figura:
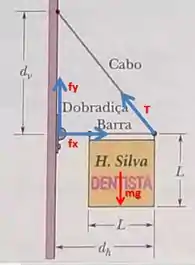
Com base nessa figura, vamos investigar o equilíbrio de torques com relação à dobradiça (das forças que agem sobre o cartaz):
Portanto:
Tal que é o ângulo que o cabo faz com a vertical. Boa lá encontrar esse ângulo então.
Passo 2
Iradoso, agora precisamos encontrar o valor de , encontramos em seguida o de , por meio da equação do passo 2. Pelo desenho podemos ver que
Como , então ,nesse caso, temos: e, consequentemente:
Passo 3
(b)Se a gente analisar o equilíbrio horizontal das forças que atuam sobre o cartaz, temos a nossa resposta:
Passo 4
(c)Como a força encontrada no passo anterior é positiva, podemos concluir que está apontada para a direita.
Passo 5
(d)Dessa vez, o equilíbrio vertical das forças que atuam sobre o cartaz nos fornece que:
Resposta
(a)
(b)
(c)Para a direita
(d)