Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 28
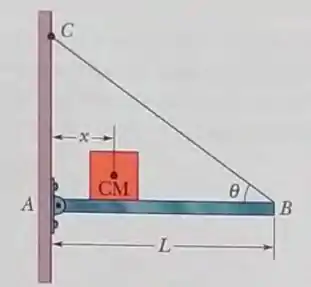
Na figura, suponha que o comprimento da barra uniforme seja e seu peso seja . Suponha ainda que o bloco tenha um peso e que O fio pode suportar uma tensão máxima de . (a) Qual é a maior distância para a qual o fio não arrebenta? Com o bloco posicionado neste valor máximo de, quais são as componentes (b) horizontal e (c) vertical da força que a dobradiça exerce sobre a barra no ponto ?
Passo 1
(a)beleza galera, vamos observar o diagrama das forças que atuam na viga:
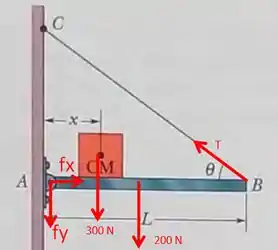
Com base nesse diagrama, podemos usar as equações de equilíbrio de torques e do somatório das forças.
Do equilíbrio de torques com relação ao ponto , temos:
tal que e são a tensão máxima na corda e o valor máximo de para que ela não seja ultrapassada. Além disso, e são o peso da viga e do bloco.
Isolando acima, a gente encontra:
Passo 2
(b)Para encontrarmos a força pedida (, basta a gente aplicar o equilíbrio horizontal das forças:
Passo 3
(c)Do equilíbrio vertical, temos:
Logo:
O valor negativo acima indica que a força está sendo aplicada para cima, em um sentido contrário ao pensado inicialmente.
Resposta
(a)
(b)
(c)