Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 82

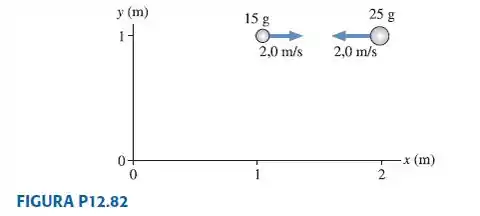
A FIGURA P12.82 mostra duas bolas de argila aproximando-se uma da outra.

a. Calcule o momentum angular total em relação à origem neste instante.

b. Calcule o momentum angular total um instante antes da colisão.

c. Calcule o momentum angular total um instante após a colisão.

Passo 1

As bolas de argila são partículas e sofrem uma colisão totalmente inelástica. O momento linear é conservado durante a colisão.

Passo 2

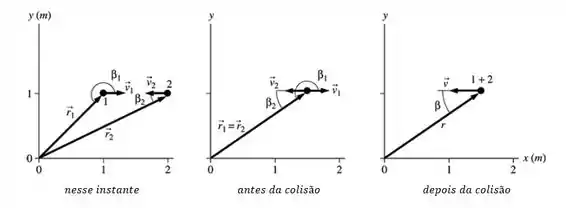
  1. O ângulo é medido no sentido anti-horário de r → a v → . Da geometria,

    2. β 1 = 180 ° + tan - 1 ⁡ ( 1 ) = 225 ° e β 2 = tan - 1 ⁡ 1 2 = 26,6 °

    Então

    L = L 1 + L 2 + m 1 r 1 v 1   s e n   β 1 + m 2 r 2 v 2   s e n   β 2

    Substituindo por números:

    L = 0,015   k g 2 m 2 m s s e n   225 ° + 0,025   k g 5   m 2,0 m s   s e n   26,6 °

    Assim,

    L = 0,020   k g   m 2 / s

    Observe que os sinais de L 1 e L 2 concordam com os determinados pela regra da mão direita.

     

    Passo 3

  2. No instante em que as bolas de barro colidem, elas estão localizadas em ( 1,5   m ,   1,0   m ) . Aqui,

    3. β 2 = tan - 1 ⁡ 2 3 = 33,7 ° β 1 = 180 ° + β 2 = 146,3 °

    Então,

    L = 0,015   k g 1,0 m 2 + 1,5 2 2,0 m s   s e n   213,7 ° + 0,025   k g 1,0 m 2 + 1,5 2 2,0 m s   s e n   33,7 ° = 0,020   k g   m 2 / s

    Passo 4

  3. As bolas de argila têm uma velocidade final v após a colisão. O momento linear é conservado.

p 1 i + p 2 i = p 1 + 2 f

Substituindo por números, temos que:

0,015   k g 2,0 m s + 0,025   k g - 2,0 m s = ( 0,015   k g + 0,025   k g v

Isso implica que

v = - 0,50   m / s .

As bolas estão se movendo para a esquerda.

Passo 3

O ângulo β = β 2 da parte (b). O momento angular após a colisão é

L = 0,040   k g 1,0 m 2 + 1,5 2 0,50 m s   s e n   33,7 ° = 0,020   k g   m 2 / s

Obs.: O momento angular também é conservado, pois τ → t o t a l = 0 .

Resposta

  1. L = 0,020   k g   m 2 / s
  2. L = 0,020   k g   m 2 / s
  3. L = 0,020   k g   m 2 / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante t , o vetor r → = 4 t 2 i → - 2 t + 6 t 2j → fornece a posição de uma partícula de 3 k g em relação à origem de um sistema de coordenadas x y ( r → está em metros e t em segundos). ( a ) E
Uma partícula de 3 , 00kg com uma velocidade de v → = 5 m / s i → - 6 m / s j → está passando pelo ponto x = 3m ,y = 8m . A partícula é puxada por uma força de 7N no sentido negativo do eixo x . Quais
Em um certo instante, a força F → = 4 j → N age sobre um objeto de 0,25 k g cujo vetor posição é r → = 2 i → - 2 k → e cujo vetor velocidade é v → = - 5 i → + 5 k → . Em relação à origem e em termos d
No instante da figura abaixo, duas partículas se movem em um plano x y . A partícula P 1 possui uma massa de 6,5 k g e uma velocidade v 1 = 2,2 m / s e está a uma distância d 1 = 1,5 m do ponto O . A
Um objeto de 2 k g que se comporta como uma partícula, se move em um plano com componentes de velocidade v x = 30 m / s e v y = 60 m / s ao passar por um ponto de coordenadas ( 3 ; - 4 ) m . Nesse ins