Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.7 - Ex. 27

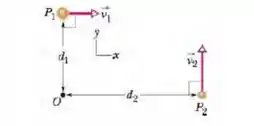
No instante da figura abaixo, duas partículas se movem em um plano x y . A partícula P 1 possui uma massa de 6,5 k g e uma velocidade v 1 = 2,2 m / s e está a uma distância d 1 = 1,5 m do ponto O . A partícula P 2 possui uma massa de 3,1 k g e uma velocidade v 2 = 3,6 m / s e está a uma distância d 2 = 2,8 m do ponto O .

Quail é

( a ) o módulo e

( b ) a orientação do momento angular resultante das duas partículas em relação ao ponto O ?

Vamos treinar momento angular? Bora lá!

Passo 1

O momento angular de um sistema vai ser dado pela soma de todos os momentos angulares de cada partícula. Sendo assim, o momento angular total aqui vai ser:

l → = l 1 → + l 2 →

Passo 2

  Agora vamos representar os vetores velocidade e posição (em relação à origem O ) de cada um em termos dos vetores unitários:

  • Para a partícula 1 :

    • r → 1 = 1,5 j →

    v → 1 = 2,2 i →

  • Para a partícula 2 :

r → 2 = 2,8 i →

v → 2 = 3,6 j →

Passo 3

Agora lembrando da definição de momento angular:

l → = m r → × v → = m . i → j → k → x y z v x v y v z

Temos como montar o produto vetorial para as duas partículas:

l → = l → 1 + l → 2 = 6,5 . i → j → k → 0 1,5 0 2,2 0 0 + 3,1 . i → j → k → 2,8 0 0 0 3,6 0

l → = 6,5 - 3,3 k → + 3,1 10,08 k → = - 21,45 k → + 31,25 k → = 9,8 k →

O módulo é 9,8 e a orientação é na direção de k → , ou seja, na direção positiva do eixo z , para fora da página.

Show!

Bora treinar mais?

Resposta

( a ) 9,8 k →

b p e r p e n d i c u l a r p a r a   f o r a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de brinquedo de 3,0k g se move ao longo de um eixo x com uma velocidade dada por v → = - 2,0 t 3 i ^m / s , com t em segundos. Para t0 , qual é (a) o momento angular L → do carro e (b) o torq
Para uma pessoa de 84 k g que se encontra no equador, qual é o módulo do seu momento angular em relação ao centro da Terra devido à rotação daTerra?
Um avião de 1200 k g está voando em uma linha reta a 80 m / s , 1,3 k m acima do solo. Qual é o módulo do momento angular do avião em relação a um ponto no solo verticalmente abaixo do local onde se e
Suponha que o ioiô do problema 17 , em vez de rolar a partir do repouso, é arremeçado para baixo com uma velocidade inicial de 1,3 m / s . ( a ) Quanto tempo o ioiô leva para chegar à extremidade da c
No instante t = 0 , o vetor posição de uma partícula de 2 k g em relação à origem é r → = 4 i → - 2 j → . A velocidade da partícula é dada por v → = - 6 t 2 i → para t ≥ 0 em segundos. Qual é ( a ) o