Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 54

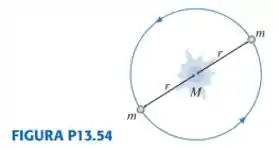
A FIGURA P13.54 mostra dois planetas de massa m orbitando uma estrela de massa M . Os planetas estão na mesma órbita, de raio r , mas estão sempre nas extremidades opostas de um diâmetro. Obtenha uma expressão exata para o período orbital T .

Passo 1

Vamos começar definindo o período orbital:

O período orbital T vai ser o tempo que esses planetas, cada um individualmente, vão levar pra dar uma volta completa ao redor da estrela e retornarem pra posição inicial mostrada na figura.

Antes da gente chegar a uma expressão pra ele, precisamos de uma expressão pra velocidade orbital desses planetas – que estamos aqui considerando idênticos: o que fazemos pra um se aplica igualmente ao outro!

Lá do capítulo de Dinâmica, estudo das forças, você viu que a força que ocasiona um movimento circular (orbital) é a força centrípeta, F c p .

Aqui no capítulo de gravitação, pra cada planeta, essa força centrípeta vai ser a força gravitacional, F g , que a estrela e o planeta diametralmente distante causam no planeta de referência.

Dando índices aos planetas, o mais à esquerda tem índice 1 e o mais à direita índice 2. A expressão pra força centrípeta, indicada pelo vetor vemelho na figura, que o planeta 1 experimenta é:

F → c p = F → g e s t r e l a + F → g p l a n e t a

Passo 2

A gente conhece a expressão pra força centrípeta e também conhece pra força gravitacional. São as seguintes:

F c p = m ∙ v 2 r

Onde m , v e r são, respectivamente, a massa do planeta que está orbitando, a velocidade orbital e a distância (raio orbital) entre o planeta e a estrela.

F g = G ∙ M ∙ m r 2

Mais especificamente, as forças gravitacionais da estrela e do planeta serão, respectivamente:

F g e s t r e l a = G ∙ M ∙ m r 2 F g p l a n e t a = G ∙ m ∙ m 4 r 2

Onde G e M são, respectivamente, a constante gravitacional universal e a massa da estrela. Os outros termos já definimos na força centrípeta são os mesmos!

Bom, como dissemos, essas duas forças, centrípeta e as gravitacionais, somadas, se equivalem aqui, logo, podemos escrever:

m ∙ v 2 r = G ∙ M ∙ m r 2 + G ∙ m ∙ m 4 r 2

Passo 3

Continuamos por desenvolver a expressão fazendo as simplificações possíveis e vamos ter:

m ∙ v 2 r = 4 ∙ G ∙ M ∙ m + G ∙ m ∙ m 4 r 2

Simplificamos os denominadores comuns da igualdade, r :

m ∙ v 2 = 4 ∙ G ∙ M ∙ m + G ∙ m ∙ m 4 r

m ∙ v 2 = G ∙ m ∙ ( 4 M + m ) 4 r

Simplificamos m , o termo comum nos numeradores:

v 2 = G ∙ ( 4 M + m ) 4 r

Obtemos uma expressão pra velocidade orbital v tirando a raiz dos dois lados:

∴ v = G ∙ ( 4 M + m ) 4 r = 1 2 G ∙ ( 4 M + m ) r

Bom, queríamos começar achando uma expressão pra velocidade orbital, e é exatamente o que acabamos de conseguir aqui!

Passo 4

Agora você vai ver que, com essa expressão pra velocidade orbital v , conseguimos uma expressão pro período orbital T .

Como a gente começou definindo, o período orbital é o tempo que um planeta leva pra dar uma volta completa ao redor de outro corpo celeste (considerando uma órbita circular).

Lá da cinemática, você sabe que a velocidade de um corpo nada mais é que a distância d que ele percorre sobre o tempo t , levado pra percorrê-la, certo? Assim:

v = d t

Pro nosso caso, de uma volta completa pela órbita circular, essa distância equivale ao comprimento da circunferência da órbita: d = 2 π r ; o tempo pra isso acontecer vale T (período), assim, t = T .

Temos assim, a seguinte expressão pra velocidade orbital:

v = 1 2 G ∙ ( 4 M + m ) r = 2 π r T

Passo 5

Como a gente quer uma expressão pro período T , basta isolar T , que vamos ter o seguinte:

1 2 G ∙ ( 4 M + m ) r = 2 π r T

T = 4 π r G ∙ ( 4 M + m ) r

Podemos reescrever o radical da seguinte forma:

T = 4 π r G ∙ ( 4 M + m ) r = 4 π r G ∙ ( 4 M + m ) r

O termo r pode ser escrito assim:

T = 4 π r G ∙ ( 4 M + m ) r = 4 π r G ∙ ( 4 M + m ) r 1 / 2

Podemos passar ele pro numerador, e assim vamos ter:

T = 4 π r G ∙ ( 4 M + m ) r 1 / 2 = 4 π r ∙ r 1 / 2 G ∙ ( 4 M + m ) =

T = 4 π ∙ r 3 / 2 G ∙ ( 4 M + m ) =

∴ T = 4 π ∙ r 3 G ∙ ( 4 M + m )

Resposta

T = 4 π ∙ r 3 G ∙ ( 4 M + m )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12.55. Muitos satélites se movem em um círculo no plano equatorial da Terra. Eles estão a uma altura tal que sempre permanecem sobre um mesmo ponto da Terra. a) Ache a altura desses satélites acima da
Os cometas descrevem órbitas elípticas em torno do Sol com elevadas excentricidades. Se um cometa possui velocidade igual a 2,0 × 10 4m / s , quando sua distancia ao centro do Sol é igual a 2,5 × 10 1
À medida que Marte percorre sua órbita elíptica em torno do Sol, sua distancia mais próxima do centro do Sol (no periélio) é igual a 2,067 × 10 11m , e sua distancia máxima ao centro so Dol (no afélio
Duas estrelas idênticas, cada uma com massa M 1 e a outra com massa M 2 , descrevem uma órbita circular em torno do centro de massa delas. A estrela de massa M 1 possui órbita com raio R 1 , e a estre
Duas estrelas idênticas, cada uma com massa M, giram em torno do centro de massa das duas estrelas. Cada órbita é circular e possui raio R, de modo que as duas estrelas estão sempre em lados opostos d