Exercícios de Órbitas em Torno do Centro de Massa - Lista de Exercícios Resolvida
Questão 1
Em um sistema binário de estrelas, duas estrelas descrevem órbitas circulares em torno de seu centro de massa comum. Se as estrelas possuem massas e e estão separadas por uma distância , mostre que o período de rotação está relacionado a através de:
Ver solução completaQuestão 2
Duas estrelas orbitam em torno de seu centro de massa comum como um sistema de estrela binária. Se cada uma de suas massas fosse dobrada, o que teria que ocorrer com a distância entre elas para que fosse mantida a mesma força gravitacional? A distância deveria:
- Permanecer a mesma
- Dobrar
- Quadruplicar
- Ser reduzida de um fator 2
- Não de pode determinar a resposta com os dados fornecidos
Questão 4
Uma estrela dupla consiste em duas estrelas de mesma massa que executam órbitas circulares de mesmo raio , mantendo-se sempre em pontos diametralmente opostos em relação ao centro de massa do sistema. A rapidez de cada estrela é
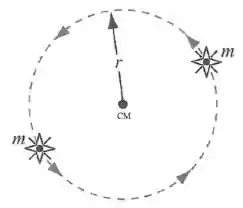
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 5
A figura ao lado mostra quatro estrelas de massa M formando um quadrado que gira em torno do centro de massa do sistema. O lado do quadrado possui comprimento L. Qual é o módulo da velocidade das estrelas? Expresse sua resposta em termos de L, M e da constante gravitacional G. Quando necessário, use
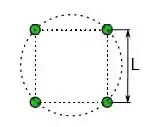
Questão 6
Um planeta com massa de está em órbita circular ao redor de uma estrela de massa . O planeta tem um raio orbital . Considerar .
a) Qual é a expressão da velocidade orbital linear do planeta, em função de
b) Qual é a expressão do período da órbita do planeta, em função de ?
c) Qual é a expressão da energia mecânica total do planeta, em função de ?
d) Qual é o valor da energia mecânica total do planeta?
Ver solução completaQuestão 7
(A) A Lua é atraída pela força gravitacional da Terra. Por que ela não se choca contra a Terra?
Ver solução completaQuestão 9
Um satélite, em uma órbita elíptica de excentricidade , tem uma velocidade no apogeu, no perigeu, e nas extremidades do semieixo menor da sua órbita. Mostre que:
(a)
(b)
A excentricidade de uma elipse é definida como a razão entre a metade da distância focal e a metade da medida do eixo maior da elipse.
Ver solução completaQuestão 10
Considere duas estrelas de nêutrons, de mesma massa , que formam um sistema binário no qual ambas giram em torno do centro de massa do sistema. Suponha também que as estrelas estão sempre em pontos opostos de uma mesma órbita circular de raio . A velocidade orbital de cada estrela em termos de , , e é:
(A)
(B)
(C)
(D)
(E)
Ver solução completa