Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.3 - Ex. 51
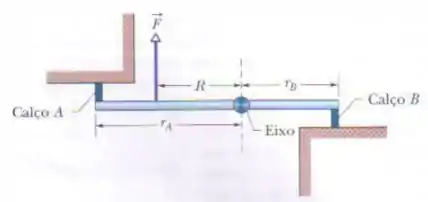
A figura é uma vista superior de uma barra rígida que gira em torno de um eixo vertical até dois que dois calços de borracha exatamente iguais, e , situados a e de distância do eixo sejam empurrados contra paredes rígidas. Inicialmente, os calços tocam as paredes sem sofrer compressão. Em seguida, uma força de módulo é aplicada perpencidularmente à barra a uma distância do eixo. Determine o módulo da força que comprime (a) o calço e (b) o calço .
Passo 1
Vamos ver se entendemos o problema. Inicialmente, os calços presos nas extremidades da barra estavam tocando a parede sem “fazer força” (sem compressão).
Depois, alguém faz uma força naquele ponto da figura, mas os calços apertam contra a parede, são comprimidos e depois não deixam ela girar mais. A pergunta é, qual é o módulo das forças em cada calço?
Beleza, como a barra não está girando, vamos começar usando as condições de equilíbrio. O torque total tem que ser zero, se não a barra ia girar.
Na fórmula do torque, as forças que empurram a barra no sentido horário ficam negativas, e as do anti-horário ficam positivas, então:
E aí:
Onde e são as forças feitas pelos calços e , respectivamente. Vamos em frente.
Passo 2
Só com essa equação não dá pra resolver o problema, porque temos duas incógnitas e uma equação só. Vamos procurar outra equação pensando na compressão dos calços.
Vamos chamar as constantes elásticas dos calços de . Lembra da fórmula da força elástica?
Dá pra aplicar isso aos calços pra achar novas equações. Vamos chamar a compressão de cada calço de e . Então:
E qual o tamanho da compressão? Veja essa imagem aqui, imagine que a reta preta representa a barra da questão, e o é o ângulo que ela faz quando
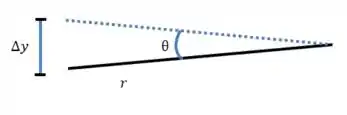
Se for bem pequeno, sabemos que dá pra dizer que . Ou seja, dá pra fazer a seguinte aproximação:
Ou sej:
Como o e o são iguais nas duas equações:
Beleza, agora vamos juntar tudo pra matar a questão.
Passo 3
Até agora temos:
Que queremos usar pra descobrir e . Então temos duas equações e duas incógnitas, então dá pra resolver.
Vamos reescrever a primeira equação:
E substituir na segunda:
E agora isolando:
E fazendo quase a mesma coisa pra achar :
Beleza, agora é só substituir.
Passo 4
Temos e , , e .
Agora ajustando pra dois algarismos significativos:
Resposta
(a)
(b)