Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 12.Problemas Adicionais - Ex. 80
A figura 1 mostra detalhes de um dos dedos da alpinista figura 2. Um tendão proveniente dos músculos do antebraço está preso na falange distal. No caminho, o tensão passa por várias estruturas fibrosas chamadas polias. A polia está presa na falange proximal; a polia está presa na falange medial. Para puxar o dedo na direção da palma da mão, os músculos do antebraço puxam o tendão, mais ou menos do mesmo modo como as cordas de uma marionete são usadas para movimentar os membros do boneco. A figura 1(b) é um diagrama simplificado da falange medial, que tem um comprimento . A força que o tendão exerce sobre o osso, , está aplicada no ponto em que o tendão entra na polia , a uma distância da extremidade da falange medial. Se as componentes das forças que agem sobre cada um dos dedos em pinça da figura 2 são e , qual é o módulo de ? O resultado é provavelmente tolerável, mas se a alpinista ficar pendurada por apenas um dos dedos, as polias e poderão se romper, um problema que frequentemente aflige os alpinistas.
Figura 1:
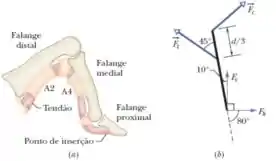
Figura 2:
Passo 1
No diagrama da figura 1(b), temos quatro forças agindo em pontos diferentes do corpo. Nesse caso, precisamos considerar o equilíbrio dos torques para garantir que o corpo esteja em equilíbrio.
Como a força é desconhecida, vamos colocar nosso ponto de referência sobre o ponto em que ela age, de forma que o seu torque será nulo. E ficamos apenas com os seguintes termos:
Em cada caso, temos que usar a seguinte fórmula para o torque:
Onde é o módulo da força, é a distância até o ponto de referência ao londo da “barra”, e é ângulo que a força forma com a “barra”.
Além disso, as forças que favorecem rotação no sentido anti-horário (em torno do nosso ponto de referência) terão torque positivo, e vice-versa.
Passo 2
Então, olhando para o desenho, vamos calcular os torques dessas três forças:
Agora vamos substituir tudo na equação de equilíbrio:
Podemos dividir tudo por e calcular o que for possível:
Resposta
O módulo de é .