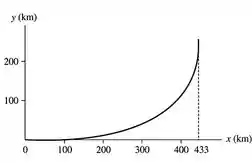
Em filmes, pilotar uma espaçonave parece fácil. Imagine-se como um estudante de física do século . Você vive em uma remota colônia espacial onde a força gravitacional devido a qualquer estrela ou planeta é desprezível. Você está indo de sua casa para a escola, deslocando-se em sua espaçonave pessoal de a , quando o computador da nave alerta para o fato de que a entrada do estacionamento está a de distância ao longo de uma linha que forma com a presente orientação de sua espaçonave, como mostra a FIGURA . Você precisa fazer uma curva à esquerda de modo a entrar no estacionamento seguindo diretamente à frente a . Você poderia conseguir isso acionando uma série de pequenos foguetes, mas você deseja impressionar as garotas na espaçonave atrás da sua passando pela entrada com um simples disparo de foguete. Você pode usar os pequenos impulsores para fazer sua nave girar rapidamente até outra orientação diferente da original e, então, ligar o foguete principal.
a. Você precisa determinar três coisas: como orientar sua espaçonave para acionar depois o foguete principal, a intensidade gerada pelo foguete e a duração da queima. Use um sistema de coordenadas em que você parte da origem e está inicialmente se movendo ao longo do eixo . Determine a orientação de sua espaçonave por meio do ângulo que ela faz com o positivo de . Sua orientação inicial é de . Você pode encerrar a queima antes de chegar à entrada, todavia é proibido passar pela entrada com o foguete ligado. A perda de massa durante a queima é desprezível.
b. Calcule as coordenadas de sua posição a cada até chegar à entrada e depois desenhe um gráfico da trajetória. Verifique se você indicou a posição da entrada.
Passo 1
Fala galera, tudo bem?
Letra a)
O impulso da queima do foguete deve ser tal que a componente da velocidade diminua de a 0 durante o mesmo intervalo em que aumenta de a . A distância horizontal que o foguete deve conseguir fazer isso é . Podemos encontrar o tempo de queima combinando duas equações cinemáticas da posição e da velocidade em função to tempo:
Da primeira equação temos:
E da segunda temos:
E a aceleração em é:
Durante esse intervalo de tempo, passa de a , então sua aceleração é:
E o vetor será dado pela segunda lei de Newton:
A intensidade é dada pela raiz da soma do quadrado das componentes:
E a orientação é:
Então devemos orientar a espaçonave na orientação de com uma força de empuxo de durante segundos.
Passo 2
Letra b)
As equações para as posições de e são:
Então a trajetória do foguete deve ser parabólica. Abaixo uma tabela com os tempos e posições relativas a cada até chegar à entrada: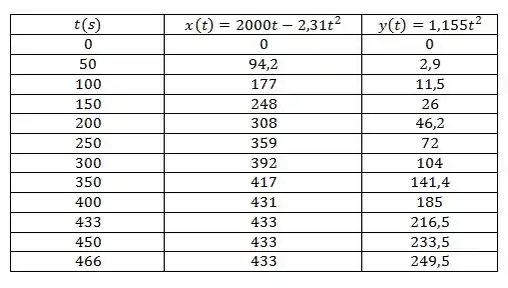
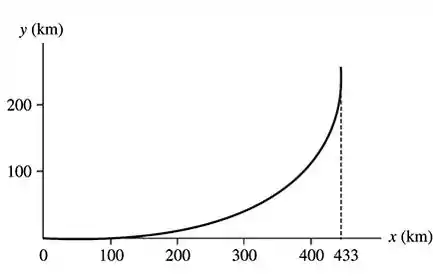
E com a ajuda de um gerador gráfico, vamos plotar um gráfico :
Como podemos ver a trajetória é realmente uma parábola onde o ponto de entrada é e .
Beleza?
Espero ter ajudado!
Vamos pra próxima?
Resposta