Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 61
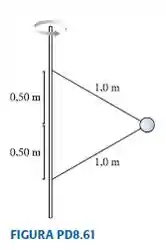
Dois arames são presos à esfera de mostrada na FIGURA . A esfera descreve um círculo horizontal com uma velocidade de módulo constante de . Quanto vale a tensão em cada arame?
Passo 1
Olá, tudo bem?
Vou ajudar você nessa aqui, vamos lá?
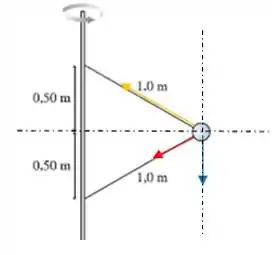O problema pede a tensão em cada fio, então precisamos de um desenho para identificar as forças agindo nesse sistema:
Sobre a bolinha agem três forças: as duas tensões (representadas em amarelo e em vermelho) e a força gravitacional (representada em azul).
Como a bolinha não tem deslocamento vertical, isso indica que nessa direção a força resultante é zero. Já na horizontal, como temos um movimento circular, a resultante das forças deve ser radial e apontar para o centro da trajetória.
Os dois arames medem cada um de comprimento, certo? E a distância entre o ponto de fixação de cada um na haste também vale (), logo o sistema todo forma um triângulo equilátero de lado ! A soma dos ângulos internos de um triângulo vale , e, como todos os lados desse triângulo são iguais, cada vértice forma um ângulo de com os lados. A linha tracejada vertical e horizontal forma um eixo de coordenadas no qual a bolinha está localizada na origem, então o ângulo entre os vetores das tensões em relação à horizontal é .
Certo até aqui?
Passo 2
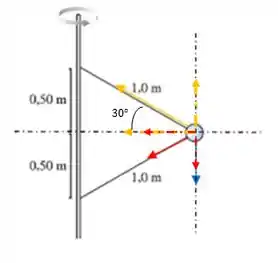Agora vou fazer um desenho com as componentes horizontal e vertical de cada força com seus respectivos ângulos pra gente visualizar melhor a situação:
Vou chamar de o módulo do vetor amarelo, o módulo vetor vermelho e o da força peso, em azul, de . A partir desse desenho, podemos formar o seguinte sistema:
Os dados que o problema nos dá são:
E o raio da trajetória? Bom, chamando de o comprimento do fio, podemos dizer que .
Beleza? Agora que temos todas as informações, precisamos resolver esse sistema. Vamos lá?
Passo 3
Partindo o sistema:
Vamos dividir a primeira equação por :
E substituindo os valores teremos:
E dividindo a segunda equação por temos:
Assim ficamos com um sistema de duas variáveis e duas equações:
Agora fazendo a soma dessas duas equações eliminamos a variável :
E usando esse valor para calcular , da primeira equação temos:
Assim as duas tensões são:
Beleza?
Espero ter ajudado!
Vamos pra próxima?