Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 49

Uma fina camada de gelo ( n = 1,309 ) flutua sobre a superficie da água ( n = 1,333 ) em um balde. Um raio de luz proveniente do fundo do balde desloca-se de baixo para cima através da água. a) Qual é o maior ângulo que o raio pode fazer com a interface água-gelo para que ele ainda passe para o ar acima do gelo? b) Qual é o ângulo depois que o gelo derrete?

Passo 1

a) fazendo um desenho para ajudar a gente:

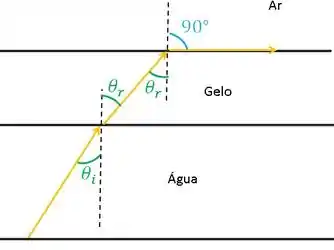
Queremos saber o θ i de tal forma que ele seja o máximo para que o raio ainda passe para a interface gelo – ar. Essa condição vai acontecer quando o θ r = θ c r i t i c o .

Aplicando a lei de snell na interface água-gelo:

n á g sen ⁡ θ i = n g sen ⁡ θ r

Aplicando a lei de snell na interface gelo-ar:

n g sen ⁡ θ r = n a r sen ⁡ 90 °

sen ⁡ θ r = n a r n g

Show!

Vamos substituir essa relação na primeira lei de snell que fizemos:

n á g sen ⁡ θ i = n g sen ⁡ θ r

n á g sen ⁡ θ i = n g n a r n g

Então:

sen ⁡ θ i = n a r n á g

Resolvendo:

θ i = 48,6 °

Uhul! Vamos pra letra b!

Passo 2

b)

agora a camada de gelo não existe mais.

Então, aplicando a lei de snell na interface água – ar:

n á g sen ⁡ θ i = n a r sen ⁡ 90 °

Então:

θ i = 48,6 °

Que é o mesmo ângulo caso a camada de gelo estivesse ali. : )

Resposta

a) θ i = 48,6 °

b) θ i = 48,6 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um raio de luz deslocando-se em um meio com velocidade v 1 parte de um ponto A e atinge um ponto B de outro meio com velocidade v 2 (Figura 33.55). O raio atinge a superficie a uma distância horizonta
Quando o Sol nasce ou se põe, ele parece estar no horizonte, porém, na realidade ele está abaixo do horizonte. A explicação para esse aparente paradoxo é que a luz se encurva ligeiramente quando penet
Um feixe de luz se deslocando de cima para baixo incide sobre uma película horizontal de espessura t , como mostra a Figura 33.57. O raio incidente divide-se em dois raios, A e B. O raio A é refletido
Um raio de luz propagando-se no ar incide com um ângulo θ a sobre a superfície superior de uma placa transparente (Figura 33.56), sendo suas duas superfícies planas e paralelas. a) Mostre que θ a = θ
Um feixe estreito de luz incide normalmente sobre uma placa grande de vidro flint de silicato formando um ângulo de 20 ° com a superficie da placa. Em virtude da dispersão, o feixe se subdivide forman