Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 57

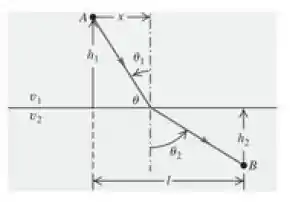
Um raio de luz deslocando-se em um meio com velocidade v 1 parte de um ponto A e atinge um ponto B de outro meio com velocidade v 2 (Figura 33.55). O raio atinge a superficie a uma distância horizontal x do ponto A. a) Demonstre que o tempo t necessário para a luz se deslocar de A até B é dado por

t = h 1 2 + x 2 v 1 + h 2 2 + l - x 2 v 2

b) Faça a derivada de t em relação a x . Iguale a zero a derivada para mostrar que esse tempo atinge o valor mínimo quando n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2 que é a lei de Snell da refração e corresponde à trajetória real do raio. Trata-se de outro exemplo do princípio de Fermat do tempo mínimo (veja o Problema 33.56).

Passo 1

a)

Nós temos a velocidade da luz nos diferentes meios, podemos descobrir a dist^cia percorrida, através dos triângulos retângulos formados nas figuras, e com isso, descobrir o tempo necessário para ir do ponto A até o ponto B.

Na primeira etapa, temos o raio de luz saindo de A e indo até a interface entre os meios. Nessa etapa, a distância percorrida é:

d 1 = x 2 + h 1 2

Na segunda etapa, temos o raio saindo da interface e indo até o ponto B.

d 2 = l - x 2 + h 2 2

Então o tempo total gasto é o tempo da primeira etapa mais o tempo da segunda etapa.

t = t 1 + t 2

Sabemos que v = d t , então:

t = d 1 v 1 + d 2 v 2

t = x 2 + h 1 2 v 1 + l - x 2 + h 2 2 v 2

Prontinho! Vamos para a próxima!

Passo 2

B

Vamos derivar...

d t d x = 2 x 2 v 1 h 1 2 + x 2 + 2 ( l - x ) ( - 1 ) 2 v 2 l - x 2 + h 2 2

Simplificando:

d t d x = x v 1 h 1 2 + x 2 - ( l - x ) v 2 l - x 2 + h 2 2

Agora, vamos igualar a derivada a zero.

x v 1 h 1 2 + x 2 - l - x v 2 l - x 2 + h 2 2 = 0

x v 1 h 1 2 + x 2 = l - x v 2 l - x 2 + h 2 2

Paraidentificarmos que essa equação é n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2 , vamos olhar na figura os senos dos ângulos:

sen ⁡ θ 1 = x h 1 2 + x 2

sen ⁡ θ 2 = l - x l - x 2 + h 2 2

Então, a equação que tínhamos fica:

sen ⁡ θ 1 v 1 =  sen ⁡ θ 2 v 2

Ok! E em relação ao v 1 e v 2 , vamos multiplicar ambos os lados da equação por c .

c sen ⁡ θ 1 v 1 = c  sen ⁡ θ 2 v 2

E agora, é só lembrar que n = c v :

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

Que é a lei de snell!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um raio de luz passa do ar para a água, atingindo a superfície da água a um ângulo de incidência de 45°. Qual, se houver alguma, das seguintes quatro quantidades varia quando a luz entra na água: (a)
A massa específica da atmosfera da Terra diminui quando aumenta a altitude. Como conseqüência, o indice de refração da atmosfera também diminui quando aumenta a altitude. Explique como podemos ver o S
Um nadador no ponto S na Figura 31-53 sente caimbra na perna enquanto esta nadando proximo a margem de um lago calmo e chama por socorro.Uma salva-vidas no ponto L escuta o chamado. A salva-vidas pode
Se o ingulo de incidencia for pequeno o suficiente,a aproximacao para angulos pequenos sen 0=0 pode ser usada para simplificar a lei da refracao de Snell.Determine o maximo valor do angulo para o qual
Luz incide em uma lâmina de material transparente a um ângulo θ 1 , como mostrado na Figura 31-60. A lâmina tem uma espessura t e um índice de refração n . Mostre que n = sen ⁡ θ 1 / sen ⁡ tan - 1 ⁡ d