Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 39

Uma esfera não condutora de raio 6,00   c m tem uma densidade volumétrica uniforme de carga 450   n C / m 3 . (a) Qual é a carga total na esfera? Determine o campo elétrico nas seguintes distâncias do centro da esfera: (b) 2,00 cm, (c) 5,90 cm, (d) 6,10 cm e (e) 10,0 cm.

Passo 1

Falaaa galera! Tudo tranquilo? Nesse exercício, queremos calcular o campo elétrico para diversos pontos de uma esfera não condutora. Essa informação de que a esfera não é condutora é muitooo importante, pois se a esfera fosse condutora toda carga extra vai para sua superfície; porém a esfera não condutora não possui essa restrição: a carga extra pode ser armazenada de qualquer forma em seu interior. Nesse caso, temos uma distribuição uniforme.

Passo 2

  1. Como a densidade é constante, a quantidade de carga será simples a densidade vezes o volume total da esfera.

    2. q = ρ V q = 450 × 10 - 9 4 3 π 0,06 3 q = 4,07 × 10 - 10   C

    Passo 3

    Para resolver os demais itens, vamos calcular o campo elétrico para pontos internos e externos da esfera:

  • Para pontos internos: para calcular o campo elétrico, a gente toma uma superfície gaussiana esférica, como mostra a figura.

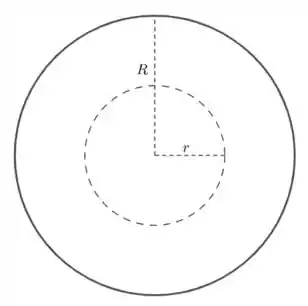
    • A carga interna será simplesmente a densidade vezes o volume da esfera gaussiana:

    q i n t = ρ 4 3 π r 3

    Porém, do item (a) a gente pode tirar que

    ρ = q 4 3 π R 3 ⟹ 4 3 π ρ = q R 3

    Assim, temos

    q i n t = 4 3 π ρ ⋅ r 3 q i n t = q r R 3

    Logo, aplicando a Lei de Gauss:

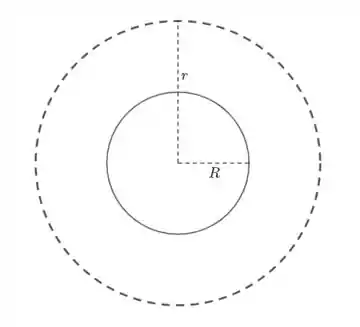
    ∮ E   d A = q i n t ε 0 E 4 π r 2 = q r 3 R 3 ε 0 ∴ E = q r 4 π ε 0 R 3

  • Para pontos externos:

Notemos que a carga interna na superfície gaussiana será a própria carga total:

q i n t = q

Logo,

E 4 π r 2 = q ε 0 E = q 4 π ε 0 r 2

Como essas duas fórmulas em mãos, poderemos resolver o problema.

Passo 3

  • Esse ponto é interno. Dessa forma, devemos aplicar a primeira relação:

    • E = q r 4 π ε 0 R 3 E = 4,07 × 10 - 10 0,02 4 π 8,85 × 10 - 12 0,06 3 = 339   N / C

  • Este também é um ponto interno. Dessa forma,

    • E = q r 4 π ε 0 R 3 E = 4,07 × 10 - 10 0,059 4 π 8,85 × 10 - 12 0,06 3 = 1,00   k N / C

  • Esse já é um ponto externo. Assim:

    • E = q 4 π ε 0 r 2 E = 4,07 × 10 - 10 4 π 8,85 × 10 - 12 0,061 2 = 983   N / C

  • Por fim, esse também é um ponto externo:

    • E = q 4 π ε 0 r 2 E = 4,07 × 10 - 10 4 π 8,85 × 10 - 12 0,10 2 = 366   N / C

    Resposta

    1. 4,07 × 10 - 10   C
    2. 3 3 9   N / C
    3. 1,00   k N / C
    4. 983   N / C
    5. 366   N / C
    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Uma esfera sólida não condutora de raio 1,00c m tem uma densidade volumétrica uniforme de carga. A magnitude do campo elétrico a 2,00c m do centro da esfera é 1,88 × 10 3N / C . (a) Qual é a densidade
    Uma esfera de raio R em densidade volumétrica de carga ρ = C / r 2 para rR onde C é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões para o campo elét
    Um cilindro sólido não condutor infinitamente longo, de raio a , tem densidade volumétrica de carga não uniforme. Esta densidade varia linearmente com a distância R , a distância perpendicular ao seu
    Um cilindro sólido de comprimento 200m e raio 6,00c m tem densidade volumétrica uniforme de carga de 300n C / m 3 . (a) Qual é a carga total do cilindro? Use as fórmulas dadas no problema 50 para calc
    Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa