Uma casca cilíndrica não condutora, infinitamente longa, com raio interno e raio externo tem densidade volumétrica uniforme de carga . Determine expressões para o campo elétrico para todas as regiões.
Passo 1
Beleza, gente? Bom, temos uma questão com simetria cilíndrica. Vamos aplicar a lei de Gauss com uma gaussiana cilíndrica.
Passo 2
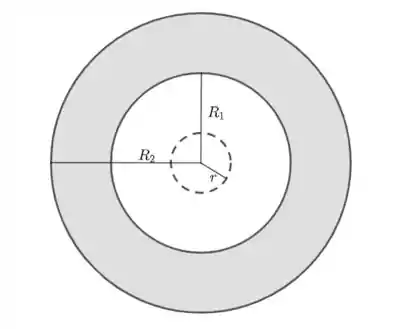
- Para : não há cargas internas, de modo que . Sendo assim, o campo elétrico é nulo nessa região.
- Para . Nesse caso, precisamos calcular a carga contida no interior. O volume será dado por:
- Para , segue que
- Para , .
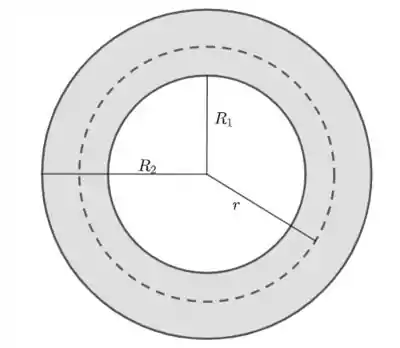
- Para ,
- Para ,
Passo 3
sendo assim,
Assim, pela lei de Gauss:
Passo 4
Aplicando a lei de Gauss, temos que
Resposta
Resposta
Ei, a resposta está no passo a passo :)