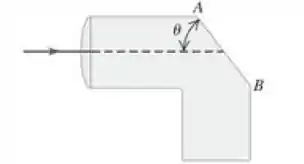
A luz entra em um tubo sólido feito de plástico e que possui um índice de refração igual a 1.60 . A luz desloca-se paralelamente à parte superior do tubo (Figura 33.40). Você deseja cortar a face A B de modo que toda a luz seja refletida de volta para dentro do tubo depois de atingir essa face. a) Qual é o maior ângulo θ possível se o tubo está no ar? b) Se o tubo for imerso em água, cujo índice de refração é 1.33 , qual é o maior ângulo θ possível?

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Exercícios - Ex. 17

A luz entra em um tubo sólido feito de plástico e que possui um índice de refração igual a . A luz desloca-se paralelamente à parte superior do tubo (Figura 33.40). Você deseja cortar a face de modo que toda a luz seja refletida de volta para dentro do tubo depois de atingir essa face. a) Qual é o maior ângulo possível se o tubo está no ar? b) Se o tubo for imerso em água, cujo índice de refração é , qual é o maior ângulo possível?

Passo 1

queremos saber o maior ângulo possível para termos uma reflexão total, ou seja o ângulo que o raio refratado faz com a normal deve ser . Certo?

Então, nesse caso, o raio incide no plástico, que tem um índice de refração , então:

Queremos saber tal que a reflexão seja total, ou seja, o raio não refrate para o ar.

E ai, acabou? Não né!! Ele quer saber esse . O que encontramos, é na verdade, o ângulo que o raio incidente faz com a normal da superfície. Mas então, com a normal faz com a superfície, sabemos que:

Logo

Agora sim!!

Vamos pra próxima.

Passo 2

b) mesma coisa de antes, mas agora o índice de refração do meio 2 será ao invés de que é o índice de refração do ar.

E o ângulo , que é o seu complementar, vale:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura 33-59, um feixe luminoso que estava se propagando no meio 1 é refratado para o meio 2, atravessa esse meio e incide com o ângulo Crítico na interface dos meios 2 e 3. Os índices de refração

Na figura 33-60, um raio luminoso penetra no ponto P, com um ângulo de incidência θ , em um prisma triangular cujo ângulo do vértice superior é 90 graus. Parte da luz é refratada no ponto Q com um âng

A figura 33-61 mostra uma fibra ótica simplificada: um núcleo de plástico n 1 = 1,58 envolvido por um revestimento de plástico com um índice de refração menos n 2 = 1,53 . Um raio luminoso incide em u

No diagrama de raios da figura 33-63 onde os ângulos não estão desenhados em escala, o raio incide com um ângulo crítico na interface dos matérias 2 e 3. O ângulo ϕ é 60° e dois dos índice de refração

Na figura 33-62, um raio luminoso incide com um ângulo θ em uma face de um cubo de plástico transparente feito de um material cijo índice de refração é 1,56. As dimensões indicadas na figura são H = 2