Um fio plástico retilíneo e não condutor de de comprimento carrega uma densidade de carga de , distribuída uniformemente ao longo do comprimento. Eles está sobre a superfície horizontal de uma mesa.
(a) Determine o módulo, a direção e o sentido do campo elétrico produzido por esse fio em um ponto diretamente acima do seu ponto médio.
(b) Se o fio for dobrado em círculo sobre a mesa, ache o módulo, a direção e o sentido do campo elétrico que ele produz em um ponto diretamente acima do seu centro.
Passo 1
(a) Temos essa situação aqui:
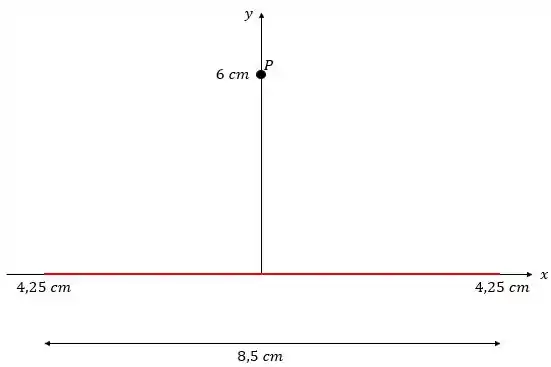
O fio está em vermelho e possui densidade linear de cargas de . Queremos saber o campo elétrico exercido porele naquele ponto ali, acima do ponto médio do fio.
Lá vem a simetria hehe. Por estar no ponto médio do fio, uma mesma quantidade de fio existe à direita e à esquerda do eixo . No caso, de fio para um lado e para outro. Com isso, as componentes do campo elétrico na direção de vão se cancelar:
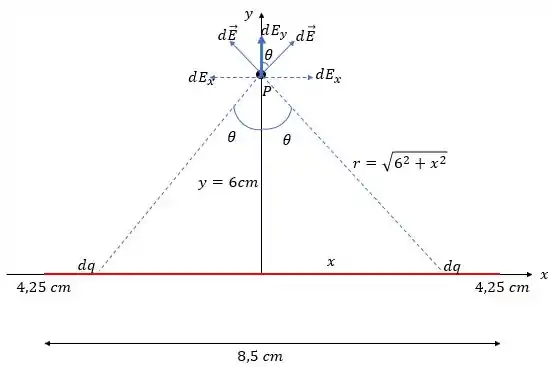
Essa é a situação do campo elétrico produzido pelo fio no ponto . Pegamos um pedaço infinitesimal do fio carregado com uma carga . Essa carga, por sua vez, vai produzir o campo , no qual sua componente será cancelada por simetria, já que do outro lado do fio existe uma outra carga para cancelar essa componente do campo. Com isso teremos campo elétrico no eixo apenas, ok?
E, pela imagem, vemos que . Onde é dado pela fórmula do campo elétrico:
Logo, substituindo:
Show! Além disso, temos que , já que é a densidade linear de cargas do fio, que está sobre o eixo . Com isso, e:
Vemos também, pela imagem, que , achamos isso fazendo Pitágoras no triângulo retângulo com o ali. Então:
Estamos quase lá! Ainda precisamos resolver esse cosseno aí. Pela imagem, vemos que . Vamos substituir mais esse cara:
AGORA SIM! Temos o valor do infinitesimal do campo elétrico produzido!! E sabemos muito bem o que fazer com um infinitesimal.... Integrar! Aqui, estamos integrando em relação ao , mas só queremos integrar sobre o tamanho do fio, né? E, pela imagem, vemos que o fio varia de até . Esses serão os nossos limites de integração:
Agora, vamos chamar o de para simbolizar o campo elétrico sobre o ponto . E podemos arrumar essa integral aí.... Repare que o termo não depende de , logo, é constante, logo, podemos jogar ele pra frente da integral:
Será que vamos precisar integrar isso aí? Relaxa, essa é uma integral bem complicada, teríamos que resolver com uma substituição trigonométrica e ninguém cobra a resolução dela. Então, não, não vamos precisar resolver essa integral. Normalmente ela é dada! A resposta é:
Essa é uma fórmula geral para o campo elétrico de um fio de tamanho a uma distância . No nosso caso, já vimos que , e .
Vamos só multiplicar toda a equação por :
E como :
Fazendo as contas:
Passo 2
(b) Se o fio foi dobrado em círculo, ele virou um anel! E aqui, queremos o campo produzido por um anel em um ponto a uma distância diretamente acima do seu centro.
A ideia para deduzir a fórmula do campo elétrico nesse caso é bem parecida com a do passo anterior. Mas, assim como a fórmula para a linha reta, a fórmula para o campo do anel também é tabelada e vale:
Onde é o raio do anel. Nós sabemos que o anel foi feito dobrando o fio, logo seu comprimento deve ser o comprimento do fio. Dessa forma:
E sabemos que e que, no problema, pede uma distância de :
E esse campo, também, estará na direção , ou seja, diretamente acima do centro do anel.
Resposta
(a)
(b)