Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 79
Uma linha infinitamente longa uniformemente carregada com carga negativa, tem densidade linear de carga igual a e está localizada no eixo . Uma pequena partícula carregada positivamente tem massa e uma carga , e está em órbita circular de raio no plano , centrada na linha de cargas. (a) Deduza uma expressão para a rapidez da partícula. (b) Obtenha uma expressão para o período da órbita da partícula.
Passo 1
A figura a seguir representa uma vista “de cima” do problema.
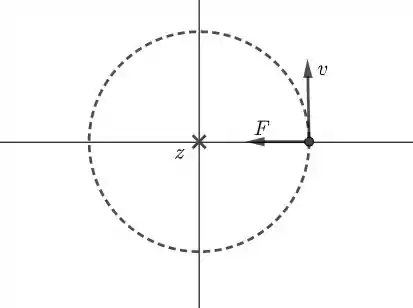
Notemos que a força elétrica entre o fio e a partícula funciona como uma força centrípeta!
Passo 2
- Temos que
- Como o movimento é uniforme, temos
Assim, temos que
o interessante a se notar é que a velocidade não depende do raio da trajetória!!
Passo 3
Resposta
Exercícios de Livros Relacionados
Um fio quadrado de lado 2 l está uniformemente carregado com densidade de carga linear λ . Calcule o campo elétrico num ponto situado sobre a perpendicular ao centro do quadrado, à distância D do seu
Um fio quadrado de lado 2 l está uniformemente carregado com densidade de carga linear λ . Calcule o campo elétrico num ponto situado sobre a perpendicular ao centro do quadrado, à distância D do seu
Uma camada infinita carregada compreendida entre os planos y = - a e y = a (fig.) tem densidade columétrica de carga ρ constante. Não há cargas fora dela. Calcule o campo elétrico E → dentro, acima e
A Figura 22-37 mostra um objeto em forma de L cujos lados têm comprimentos iguais. Uma carga positiva está distribuída uniformemente ao longo do comprimento do objeto. Quais são a direção e o sentido
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri