Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 78

Uma lâmina plana infinita não condutora está no plano x = 2,00   m e tem densidade superficial uniforme de carga + 2,00   μ C / m 2 . Uma linha infinita carregada e não condutora, com densidade linear uniforme de carga igual a 4,00   μ C / m , passa pela origem em um ângulo de 45,0 ° com o eixo x no plano x y . Uma esfera sólida não conduta com densidade volumétrica de carga - 6,00   μ C / m 3 e raio 0,800   m está centrada no eixo x em x = 1,00   m . Calcule a magnitude, a direção e o sentido do campo elétrico no plano z = 0 em x = 1,50   m e y = 0,50   m

Passo 1

Vamos calcular o campo de cada elemento separadamente.

  • Campo devido o fio:

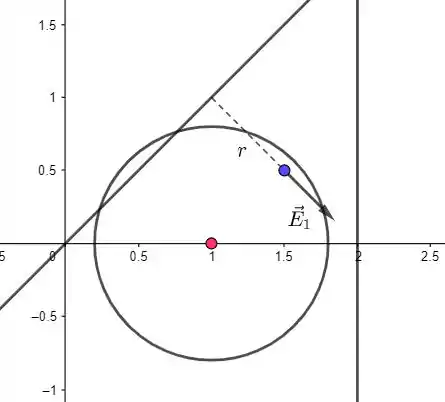
    • O módulo do campo elétrico será:

    E 1 = λ 2 π ε 0 r

    Então, precisamos calcular r . Existe uma forma de se calcular a distância de um ponto até uma reta. Veja que a equação da reta é simplesmente x = y , ou seja, x - y = 0 . Queremos a distância de P = 1,50   ; 0,50 até essa reta. No geral, a distância de um ponto P = x 0 , y 0 até a reta a x + b y + c = 0 é:

    r = a x 0 + b y 0 + c a 2 + b 2

    Aplicando essa fórmula, com a = 1 , b = - 1 , c = 0 , x 0 = 1,50   e y 0 = 0,50 , temos:

    r = 1,50 - 0,50 2 = 1 2 ≈ 0,71   m

    Em termos vetoriais, temos que

    E → 1 = E 1 cos ⁡ 45 ° i ^ - sen ⁡ 45 ° j ^ = 8,85 × 10 - 12 2 π 8,85 × 10 - 12 0,71 cos ⁡ 45 ° i ^ - sen ⁡ 45 ° j ^ E → 1 = 71,90   k N / C i ^ + - 71,90   k N / C j ^

    Passo 2

  • Cálculo do campo devido ao plano

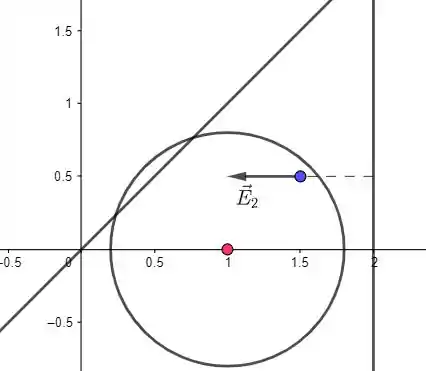
    • Temos que

    E → 2 = - σ 2 ε 0 i ^ = - 2,00 × 10 - 6 2 8,85 × 10 - 12 = - 112,9   k N / C i ^

    Passo 3

  • Cálculo do campo devido a esfera:

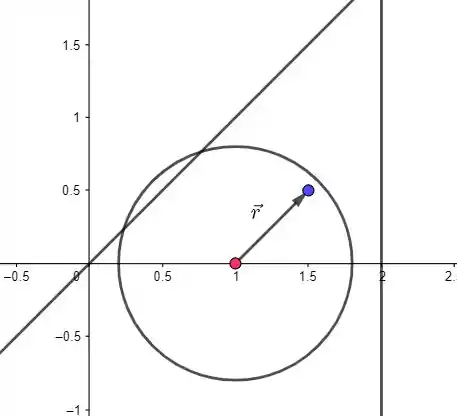
Sabemos que o campo elétrico no interior de uma esfera uniformemente carregada (e não condutora) é dado por:

E → 3 = ρ 3 ε 0 r →

Como

r → = 0,50   m i ^ + 0,50   m j ^

Segue que

E → 3 = - 6,00 × 10 - 6 3 8,85 × 10 - 12 0,50 i ^ + 0,50 j ^ E → 3 = - 113   k N / C i ^ + - 113   k N / C j ^

Passo 2

Dessa forma, o campo elétrico total é

E → = E → 1 + E → 2 + E → 3 E → = - 154,0   k N / C i ^ + - 184,9   k N / C j ^

O módulo será dado por:

E = 154 2 + 184,9 2 = 241   k N / C

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Uma linha de cargas com densidade linear uniforme λ está sobre o eixo x desde x = 0 até x = a . Mostre que a componente y do campo elétrico em um ponto do eixo y é dada por y = k λ y a y 2 + a 2 , y ≠
Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitas linhas retas de carga.