Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 70

Uma fina lâmina infinita no plano y = 0 tem densidade superficial de carga σ 1 = + 65   n C / m 2 . Uma segunda fina lâmina infinita tem densidade uniforme de carga σ 2 = + 45   n C / m 2 , intercepta o plano y = 0 no eixo z e faz um ângulo de 30 ° com o plano x z , como mostra a figura 22-45. Determine o campo elétrico em (a) x = 6,0   m , y = 2,0   m e (b) x = 6,0   m e y = 5,0   m .

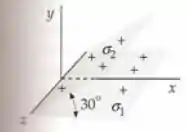
Passo 1

Fala galera, beleza? Essa questão tem uma visão geométrica um pouquinho complicada. Mas vamos tentar fazer com calma.

Passo 2

  1. O plano x z faz um campo elétrico na direção de y . Vamos olhar o outro plano. Veja a figura abaixo:

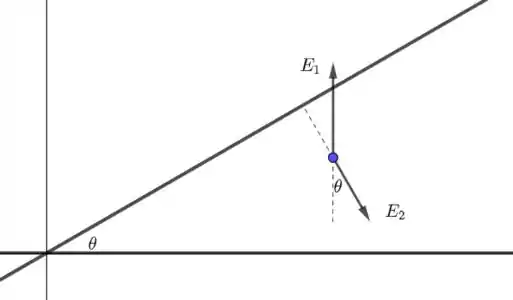
    2. Na figura, ilustramos o plano x y . E 1 é o campo elétrico devido ao plano x z e E 2 devido ao plano inclinado.

    E → 1 = σ 1 2 ε 0 j ^ = 3,67   k N / C j ^

    E também,

    E → 2 = σ 2 2 ε 0 sen ⁡ θ i ^ - cos ⁡ θ j ^ = 1,27   k N / C   i ^ + - 2,20   k N / C   j ^

    Dessa forma,

    E → = E → 1 + E → 2 = 1,27   k N / C   i ^ + 1,47   k N / C   j ^

    Passo 3

  2. A única diferença é que E → 2 terá o sentido contrário agora.

E → 2 = - 1,27   k N / C   i ^ + 2,20   k N / C j ^

Logo,

E → = E → 1 + E → 2 = - 1,27   k N / C   i ^ + 5,87   k N / C   j ^

Resposta

  1. 1,27   k N / C   i ^ + 1,47   k N / C   j ^
  2. - 1,27   k N / C   i ^ + 5,87   k N / C   j ^
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma carga puntiforme q é colocada numa caixa cúbica de aresta l . Calcule o fluxo do campo elétrico sobre cada uma das faces se a carga ocupa o centro do cubo.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Uma carga puntiforme q é colocada numa caixa cúbica de aresta l . Calcule o fluxo do campo elétrico sobre cada uma das faces se a carga está num dos vértices.
Um fio de comprimento l está uniformemente carregado com densidade linear de carga λ .Calcule o campo elétrico num ponto situado sobre o prolongamento do fio, a uma distância d da sua extremidade.Calc
Dois fios retilíneos de mesmo comprimento a , separados por uma distância b , estão uniformemente carregados com densidade lineares de carga λ e - λ (fig.) Calcule o campo elétrico no centro P do retâ