Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 6

Um fio quadrado de lado 2 l está uniformemente carregado com densidade de carga linear λ . Calcule o campo elétrico num ponto situado sobre a perpendicular ao centro do quadrado, à distância D do seu plano (fig.).

Sugestão: Use componentes cartesianas e considerações de simetria.

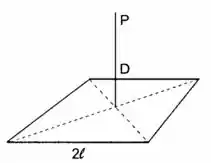
Passo 1

Se liga! Primeiro vamos separar os segmentos do quadrado em 4 partes e pensar nas simetrias!

Olha a figura!

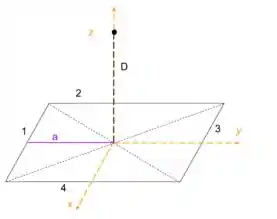
Podemos reparar que existe simetria em relação ao eixo x entre os segmentos 1 e 3 e em relação ao eixo y é entre os segmentos 2 e 4.

Agora vamos pegar o pedaço 1 e analisar o campo que ele exerce sobre o ponto. Veja a figura.

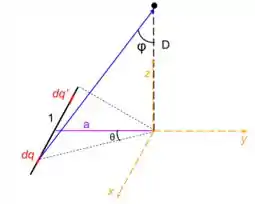
Podemos notar que o campo exercido sobre o ponto pelo elemento infinitesimal d q tem componentes na 3 direções e o produzido pela elemento d q ' também. Entretando, ao somar os campos produzidos pelos dois elementos, por serem simétricos em relação ao eixo y , as componentes na direção x dos campos se anulam, sobrando apenas as componentes nos eixos y e z .

Passo 2

Se pegarmos os lados 1 e 3, perceberemos que exite uma simetria em relação ao eixo x que fará com que as componentes em y das campos gerados por esses dois lados se anulem. Restando assim, apenas a força na direção z .

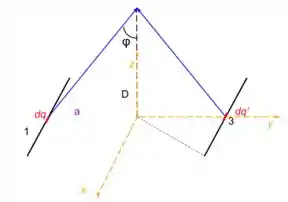
Passo 3

Podemos fazer os mesmos passos para os lados 2 e 4, e chegaremos a conclusão que novamente só restará a campo na direção z .

Sendo assim, se calcularmos a componente E z de um dos lados e depois multiplicar o valor por 4 e teremos o campo sobre o ponto.

Sabendo que o campo exercido por um elemento infinitesimal é

E = k d q d 2

Onde

d 2 = D 2 + x 2 + l 2 ;

λ = d q d x   ⇒ d q = λ d x

Substituindo na expressão do campo temos

E = k λ   d x D 2 + x 2 + l 2

Como queremos apenas a componente z ,

d E z = k λ   d x D 2 + x 2 + l 2 cos ⁡ φ

Podemos escrever

c o s φ = D D 2 + x 2 + l 2 1 / 2

Substituindo na última expressão do campo, teremos

d E z = k D λ   d x D 2 + x 2 + l 2 3 / 2

Passo 4

Para achar o campo produzido pelo fio inteiro, basta integrarmos d E z

Sabemos que x vai variar de - l até l . Sendo assim, o campo do fio produzido pelo fio fica

E z = k λ D ∫ - l l   d x D 2 + x 2 + l 2 3 / 2 Agora precisamos resolver a integral, certo?! Essa integral é tabelada! Pela tabela temos

∫ d u a 2 + u 2 3 / 2 =   u a 2 a 2 + u 2 + C

Sendo assim, empregando os intervalos de integração teremos E z = 2 k λ D D 2 + l 2 l D 2 + 2 l 2

Como já foi falado, para pegar o campo produzido por todos os lados, devemos multiplicar por 4. Substituindo

k = 1 4 π ϵ o

Temos

E z = 2 λ D π ϵ 0 ( D 2 + l 2 ) l D 2 + 2 l 2

E ele aponta no sentido positivo de z . Portanto

E z → =   λ π ϵ 0 b a a 2 + b 2     z ^

Resposta

E z → =   λ π ϵ 0 b a a 2 + b 2     z ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A que distancia ao longo do eixo central de um anel de raio R, carregado uniformemente, o modulo do campo elétrico é máximo?
Na Fig. 24-34, duas barras finas de plástico, uma de carga +q e a outra de carga −q, formam um círculo de raio R num plano xy. Um eixo x passa pelos pontos que unem as duas barras e a carga em cada um
Uma barra fina, não-condutora, de comprimento finito L, tem uma carga q uniformemente distribuída ao longo dela. Mostre que o módulo E do campo elétrico no ponto P sobre a mediatriz da barra é dado po
Um elétron tem seu movimento restrito ao eixo central do anel de carga de raio R discutido na Seção 24-6. Mostre que a força eletrostática exercida sobre o elétron pode fazê-lo oscilar através do cent
Na Fig. 24-37, uma barra não-condutora, de comprimento L, tem uma carga -q uniformemente distribuída ao longo de seu comprimento. (a) Qual a densidade linear de carga da barra? (b) Qual o campo elétri