Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 5
Fique em pé no centro de uma sala grande. Chame a direção à sua direita de “positiva” e a direção à sua esquerda de “negativa”. Ande ao longo da sala em uma linha reta, usando uma aceleração constante para atingir em pouco tempo uma rapidez fixa ao longo de uma reta na direção negativa. Após atingir essa rapidez, mantenha sua velocidade negativa, mas faça sua aceleração positiva. (a) descreva como sua rapidez variou conforme você andava. (b) Esboce um gráfico de em função de para o seu movimento. Presuma que você começou em . (c) Diretamente sob o gráfico da parte (b), esboce o gráfico de em função de .
Passo 1
Olá! E aí? Então, você está numa sala grande. Ele pede para a gente pensar para a direita, o sentido é positivo e para esquerda, temos o sentido negativo. Desenhando, seria algo assim:
A ideia do enunciado é que você vai estar parado, depois vai dar uma “corridinha” (vai acelerar) para a esquerda (o sentido que ele chama de nagativo) até atingir uma certa rapidez.
Ele diz que essa rapidez é fixa, então vamos considerar que essa rapidez fica constante por um tempinho. Ou seja, cê anda com essa rapidez fixa por um tempo.
Depois, você vai continuar andando na mesma direção, no sentido negativo. Isso porque ele fala para você manter uma velocidade negativa, como a velocidade dita a direção e sentido do movimento, você vai estar no sentido negativo, ou seja, continuar para a esquerda.
Só que ele fala para você ter uma aceleração positiva. Como a sua velocidade é negativa, temos que a velocidade e a aceleração terão sentidos opostos, o que faz com que a velocidade vá diminuindo em módulo, ou seja, você vai andar para a esquerda, mas cada vez mais devagar.
Agora que a gente viu o que aconteceu, vamos fazer o que ele pede em cada item!
Passo 2
(a) Como fica a sua rapidez ao longo desse movimento? Como você começou parado, ela era nula, e então aumentou de maneira uniforme, porque sua aceleração era constante.
Depois ela atingiu um valor fixo e que você fica nele por um tempo, então a rapidez é constante por um tempinho.
Vimos que depois há uma aceleração positiva, o que fez com que a velocidade em módulo diminuísse, o que faz também com que a rapidez diminua.
Assim, depois de aumentar uniformemente, a rapidez atingiu um certo valor, ficou constante nele, e então começou a diminuir (não sabemos se de forma uniforme ou não, porque não sabemos se a aceleração positiva é constante).
Perceba que, quando pensamos na rapidez não precisamos nos preocupar com o sentido em que começamos o movimento (positivo ou negativo), o mesmo não acontece com a velocidade.
Passo 3
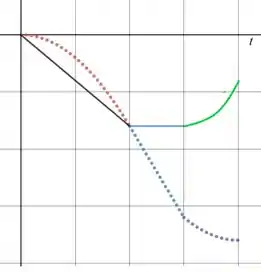
(b) Vamos fazer um gráfico de em função de . Estamos sempre andando na direção negativa, então nosso valor de sempre diminui, tudo bem?
Quando tivermos aceleração constante, no primeiro intervalo de tempo, o gráfico da posição vai ter um formato de parábola, pois vai seguir uma equação desse tipo:
Onde e são constantes. Como a aceleração é negativa, nossa parábola vai ter concavidade para baixo.
Quando tivermos aceleração nula (rapidez constante), no segundo intervalo de tempo, o gráfico vai ser uma reta, pois vai seguir uma equação desse tipo:
Onde é constante.
E no intervalo final, o objeto começa a desacelerar, mas não chega a inverter seu sentido do movimento, porque a velocidade continua negativa, então continua diminuindo.
Percebe que esse final não é uma parábola exatamente porque a gente não sabe se a aceleração é constante.
Passo 4
(c) Agora vamos fazer um gráfico da velocidade em função do tempo.
Saímos de zero porque saímos do repouso.
No primeiro momento temos uma aceleração constante no sentido negativo. A relação entre velocidade e tempo quando temos uma aceleração constante é linear, então vamos ter uma reta inclinada para baixo (porque a velocidade está diminuindo).
No segundo intervalo temos uma reta horizontal porque a rapidez é constante em um sentido, lembra? Logo, a velocidade é constante também e fica em um valor fixo.
E no fim, temos uma aceleração positiva, que vimos que vai diminuir nossa velocidade em módulo, ou seja, a velocidade vai ser aproximando de zero. Como a gente não sabe se a aceleração é constante, vamos fazer uma curva genérica se aproximando de zero conforme aumenta.
O gráfico fica:
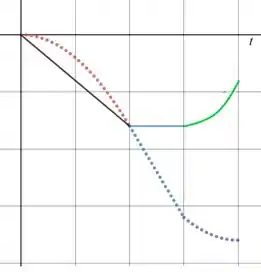
Resposta
(a) A rapidez começa nula, atinge um valor onde fica constante e então começa a diminuir.
(b)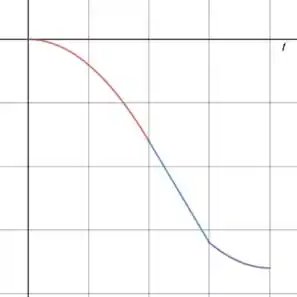 
(c) 