Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 12

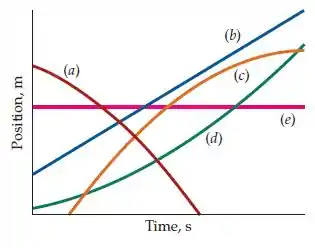
Qual das curvas de posição em função do tempo na figura abaixo melhor representam o movimento de um objeto (a) com aceleração positiva, (b) com velocidade constante positiva, (c) que está sempre em repouso e (d) com aceleração negativa. (Pode haver mais de uma resposta correta para cada item).

Passo 1

(a) Já que estamos falando de posição em função do tempo, vamos dar uma olhada na equação horária da posição:

x t = x 0 + v 0 t + 1 2 a t 2

Quando tivermos aceleração positiva ( a > 0 ), esperamos que o gráfico seja uma parábola com a abertura voltada para cima, que o gráfico representado por d .

Passo 2

(b) Se o objeto tem velocidade constante positiva, nós temos a = 0 e v 0 > 0 , então:

x t = x 0 + v 0 t

Que deve ser uma reta com inclinação positiva, que está representado pelo gráfico ( b ) .

Passo 3

(c) Se o objeto está sempre em repouso, então a = v 0 = 0 , e a equação é:

x t = x 0

E o gráfico será uma função constante, que é o caso de ( e ) .

Passo 4

Se o gráfico tem aceleração negativa, então a equação é:

x t = x 0 + v 0 t + 1 2 a t 2

Mas com a < 0 , ou seja, teremos uma parábola com a abertura voltada para baixo. Nesse caso, os gráficos ( a ) e   ( c )   servem, porque são apenas trechos diferentes de uma parábola desse tipo.

Resposta

(a) Gráfico d ; (b) Gráfico b ; (c) Gráfico e ; (d) Gráficos a e c .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A posição de um corpo oscilando em uma mola é dada por x = A sen ⁡ ω t , onde A e ω são constantes. A = 5,0c m , e ω = 0,175s - 1 . (a) Plote x como uma função de t para 0 ≤ t ≤ 36s . (b) Meça a incli
Partindo de uma estação, um trem de metrô acelera a partir do repouso à taxa constante de 1,00 m/s² na metade do percurso até a estação seguinte, e depois freia à mesma taxa no resto do percurso. A di
Um corredor, viajando com a rapidez constante de 125 km/h, passa por um cartaz. Um carro-patrula parte do repouso, com aceleração constante de (80 km/h)/s até atingir sua rapidez máxima de 190 km/h, q
Um trem parte de uma estação com uma aceleração constante de 0,40 m/s². Uma passageira chega a um ponto junto ao trilho 6,0 s após o final do trem ter passado pelo mesmo ponto. Qual é a menor rapidez
Uma gazela está correndo em linha reta ( oe i x ox ). O gráfico na Figura 2.45 mostra a velocidade desse animal em função do tempo. Nos primeiros 12,0s , determine a) A distânciatotal percorrida e b)