Em física de partículas, a energia potencial associada com um par de quarks ligado pela força nuclear forte é, em um particular modelo teórico, escrita como a função , onde e são constantes positivas, e é a distância de separação entre os dois quarks. (a) Esboce a forma geral da função da energia potencial. (b) Qual é a forma geral para a força que cada quark exerce sobre o outro? (c) Para os casos extremos de valores de muito pequenos e muito grandes, a força toma qual forma simplificada?
Passo 1
O primeiro passo é simplesmente usar algum programa para esboçar o gráfico da seguinte função que foi dada no enunciado:
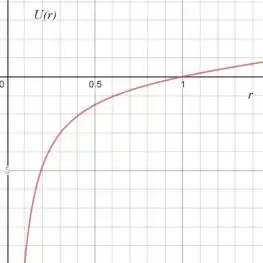
Passo 2
(b) Agora queremos encontrar a expressão geral para a força. Para fazer isso a partir do potencial só precisamos lembrar da seguinte relação:
E agora é só aplicar as regras de derivação que já conhecemos bem. Cuidado para não se confundir com os sinais!
Passo 3
(c) Vamos analisar os casos extremos da força.
Quando é muito grande, a fração tende a zero, então:
E quando é muito pequeno, a fração tende a um valor muito alto, ao ponto em que o se torna desprezível:
Resposta
(a) Gráfico.
(b) .
(c) Para muito grande, , para muito grande .