Pêndulo. Uma pedra com massa de está presa a um fio de comprimento, de massa desprezível, formando um pêndulo. O pêndulo oscila até um ângulo de com a vertical. Despreze a resistência do ar.
a) Qual é a velocidade da pedra quando ela passa pela posição vertical? b) Qual é a tensão no fio quando ele faz um ângulo de 45° com a vertical? c) Qual é a tensão no fio quando ele passa pela posição vertical?
Passo 1
Oi, galerinha! Tudo bom? O enunciado nos fala sobre um pêndulo composto de um fio de massa desprezível e que oscila até um ângulo de 45º graus. Para resolvermos iremos usar a conservação de energia e fazer a decomposição de forças no ponto A, que será o ponto onde a pedra está na vertical.
Se liga nesse esqueminha:
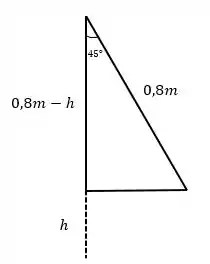
Lembrando, que conforme a pedra do pendulo está descendo, ela está ganhando velocidade. Ou seja, sua energia potencial está sendo convertida em energia cinética.
Passo 2
(a) Inicialmente, vamos estabelecer que no ponto onde a pedra está na vertical, a altura será e que no ponto mais alto, onde o ângulo é de 45º graus, a velocidade é . Assim, temos a seguinte conservação de energia:
Mas qual a altura ?
Passo 3
Vamos trazer pra pertinho o esquema que a gente fez:
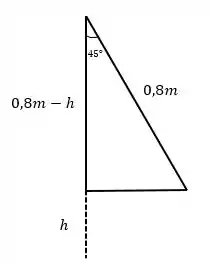
Então, a altura pode ser calculada por:
Isolando :
Passo 4
Opa, agora que temos a altura quando o pêndulo faz !!
Substituindo os valores na equação para a conservação de energia:
Isolando a velocidade final:
Então, essa é a velocidade da pedra na posição vertical.
Passo 5
(b) Temos que a graus, a velocidade é e não haverá aceleração centrípeta, assim a tensão será igual a componente da força peso nessa direção.
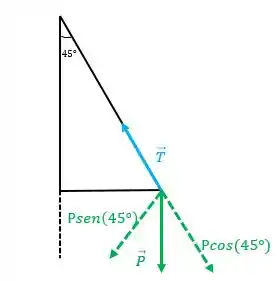
Então:
Passo 6
(c) Nessa posição haverá uma resultante do movimento, que será a centrípeta na direção da tensão, isso porque o pêndulo não está em repouso, já que ele vem caindo com uma velocidade e aceleração. Assim teremos:
Como a aceleração centrípeta é dada pela divisão do quadrado da velocidade linear pelo raio da trajetória, que seria o próprio tamanho do pêndulo:
Prontinho!
Resposta
c)