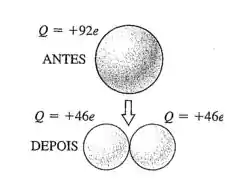
Fissão nuclear. O núcleo instável de urânio 236 pode ser considerado uma esfera uniformemente carregada com carga e raio . Em uma fissão nuclear, ele pode se subdividir em dois núcleos menores, cada um deles com a metade da carga e a metade do volume do núcleo de urânio 236 original. Essa foi uma das reações que ocorreram durante a explosão da bomba atômica em Hiroshima, no Japão, em agosto de 1945. (a) Determine os raios de dois núcleos ‘filhos’, cada um deles com carga . (b) Como modelo simples do processo de fissão, imaginamos que, imediatamente após a fissão, os dois núcleos ‘filhos’ estão em repouso e quase em contato, conforme mostra a Figura 23.41. Calcule a energia cinética de cada núcleo ‘filho’ quando a distância entre eles é muito grande. (c) Nesse modelo, a soma da energia cinética de cada núcleo ‘filho’ calculada no item (b) é a energia liberada pela fissão do núcleo de urânio 236. Calcule a energia liberada pela fissão de 10,0 kg de urânio 236. A massa atômica do urânio 236 é igual a 236 u, em que 1 u=1 unidade de massa atômica =. Expresse sua resposta em joules e em quilotons de TNT ( 1 quiloton de TNT libera durante sua explosão. (d) Com base nesse modelo, discuta por que razão uma bomba atômica poderia também ser chamada de ‘bomba elétrica’.

letra b)

Para calcular a energia cinética podemos usar conservação de energia!

Como queremos a energia cinética para cada núcleo filho teremos então:

letra c)

Podemos escrever a energia liberada em termos da energia potencial através da relação:

é o número de núcleos que há em de urânio.

Podemos determinar pela relação:

A energia então será:

letra d)

Poderíamos chamar de bomba elétrica porque a energia potencial elétrica que fornece energia elétrica para a partícula.