Um fogo de artifício é posto dentro de um coco e o explode em três pedaços. Dois deles são de mesma massa e saem para o sul e o oeste, perpendicularmente um ao outro, a . O terceiro pedaço tem o dobro da massa dos outros. Quanto vale o módulo e qual é a orientação da velocidade com que sai o terceiro pedaço? Represente a orientação como um ângulo a nordeste

Vamos desenhar as três partículas que compõem o coco da seguinte forma:

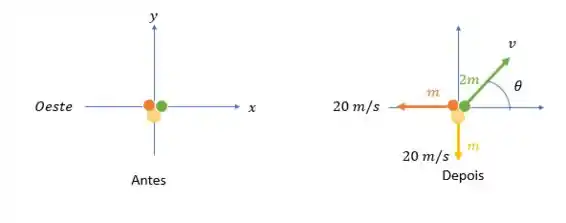Pela conservação do momento linear temos que:

E como não há movimento de nenhuma das partículas nós temos que o momento linear inicial é nulo, ou seja . Então (considerando partícula 1 a de cor laranja, partícula 2 a amarela e partícula 3 a verde nós teremos):

Onde . (Temos que espelhar em todas as direções a velocidade, e sabe-se da álgebra que é a direção unitária do eixo e a direção unitária no eixo e consideramos como o módulo da velocidade da partícula 3). Então a conservação do momento nos dará:

Isso nos dá: