Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 46
Um foguete meteorológico de acelera para cima a . Passados da decolagem, o foguete explode e divide-se em dois pedaços, um com o dobro da massa do outro. Fotos tiradas revelam que o fragmento mais leve deslocou-se diretamente para cima e atingiu uma altura máxima de . Qual era o módulo e qual era a orientação da velocidade do fragmento mais pesado logo após a explosão?
Passo 1
Fazendo o diagrama do foguete meteorológico antes e depois da explosão nós teremos:
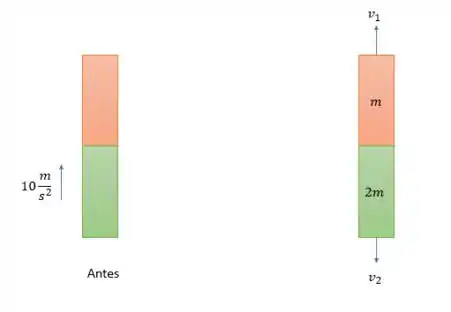
Antes da explosão o corpo estava com uma velocidade vertical de e a altura atingida seria de:
Supondo que ela parte do repouso , então a altura será de:
Agora para a conservação de momento linear de antes e depois da explosão:
Lembrando que o sinal positivo de é ele apontando para baixo tal como está na figura.
Logo pela conservação do momento linear teremos:
Passo 2
Agora vamos utilizar a informação que a massa menor sobe com a explosão, e como inicialmente ela está com uma velocidade inicial de e quando se tem a altura máxima então a velocidade chega a zero então por Torricelli teremos:
Pois somente a gravidade vai desacelerar o corpo. (Não temos mais influência dos causados pelo foguete)
Pois o corpo menor atinge uma altura máxima de sendo que ele já estava acima do solo.
Então a velocidade do corpo (pela equação da conservação do momento do passo 1) será:
Isso diz que o corpo maior cai após a explosão.
Resposta
Apontando para o chão.