Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 8.Problemas - Ex. 94
Um foguete de fogos de artifício é disparado verticalmente de baixo para cima com velocidade de e direção de acima da horizontal. Durante o voo, o foguete explode e se parte em dois pedaços de mesma massa (ver Figura ). (a) Qual é a distância horizontal desde o ponto de lançamento que o centro de massa das duas partes estará após elas terem parado no solo? (b) Se uma parte parar a uma distância horizontal de do ponto de lançamento, onde a outra parte parará?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinara a distância horizontal desde o ponto de lançamento que o centro de massa das duas partes estará após elas terem parado no solo e (b) considerando que uma parte pare a uma distância horizontal de do ponto de lançamento, onde a outra parte parará.
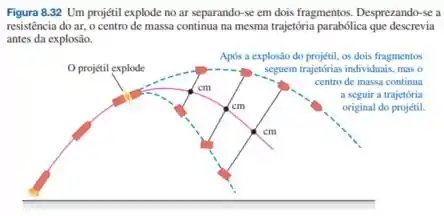
Esse é um exercício bem legal sobre lançamento oblíquo misturado com conservação da quantidade de movimento. Eu atiro um projétil com uma velocidade inicial com um ângulo de lançamento com relação a horizontal e ele executaria um movimento parabólico perfeito caso não explodisse em duas partes.
No item (a) queremos saber o alcance horizontal do centro de massa do sistema. Como você pode ver na figura e deve ter estudado ao longo do capítulo, o centro de massa do sistema executa o movimento parabólico que o projétil descreveria se não tivesse explodido em partes. Com isso, para resolver o item (a), basta considerar um problema tradicional de lançamento oblíquo!
A fórmula do alcance máximo é dada por
No próximo eu vou deduzir essa expressão com cuidado. Caso você já saiba fazer isso e não tenha interesse em acompanhar a dedução, pule para o passo !
Vamos lá!
Passo 2
O primeiro passo é decompor o vetor velocidade inicial:
Na vertical temos um movimento de lançamento vertical com aceleração para baixo. Com isso, podemos achar o tempo de subida usando
No ponto mais alto da trajetória, temos e , de modo que
O tempo total de voo vai ser o dobro do tempo de subida. Assim,
Na horizontal temos um movimento uniforme, de modo que o alcance será
Usando que , achamos que
Passo 3
Agora é só substituir os valores para achar o alcance do centro de massa:
Portanto,
Passo 4
Para fazer o item (b), basta comparar as posições de queda de cada pedaço com a posição do centro de massa:
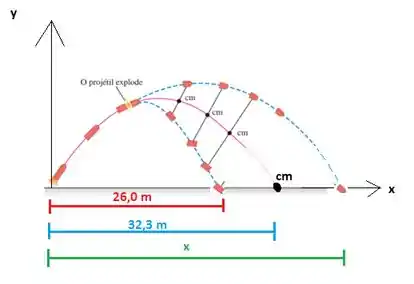
A posição do centro de massa é
Como , temos que
Logo,
Resolvendo a equação, achamos
Valeu, galera! Até a próxima! 😉