Um haltere assimétrico consiste em uma barra uniforme de de comprimento e de massa. Em uma extremidade há uma esfera sólida uniforme de de diâmetro e de massa, e na outra extremidade há uma esfera sólida uniforme de diâmetro e 750 g de massa. (A distância centro-a-centro entre as esferas é de .) (a) Onde, em relação ao centro da esfera leve, está o centro de massa do haltere? (b) Se este haltere é atirado para cima (mas girando em tomo de si), de forma que a rapidez inicial de seu centro de massa é , qual é a velocidade do centro de massa depois? (c) Qual é a força externa resultante sobre o haltere enquanto no ar? (d) Qual é a aceleração do centro de massa do haltere após o lançamento?
Passo 1
A representação abaixo resume as informações sobre o bastão desequilibrado e mostra uma escolha conveniente para uma coordenada sistema.
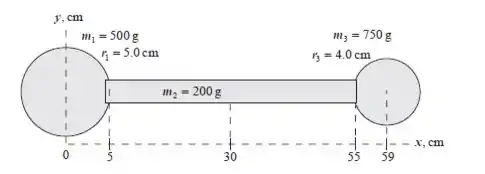
Passo 2
Item (a)
A coordenada do centro de massa do bastão desequilibrado é dado por:
Substituindo por valores numéricos:
Passo 3
Item (b)
Porque o centro de massa do bastão age como uma partícula pontual, usando a equação de aceleração constante para expressar a velocidade como uma função de tempo:
Como a aceleração :
Substituindo por valores numéricos e fazendo :
Passo 4
Item (c)
A força resultante externa agindo sobre o bastão é a força gravitacional (peso) exercido pela Terra:
Substituindo por valores numéricos:
Passo 5
Item (d)
Mais uma vez, como o centro de massa age como uma partícula pontual, sua
aceleração é a de uma partícula pontual em voo perto da superfície da Terra: