Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 138

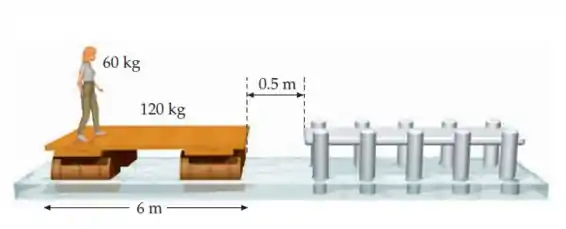
Você está de pé bem na traseira de uma balsa de 6,0 m de comprimento e 120   k g de massa que está parada em um lago, com a proa apenas a 0,50   m da borda do píer (Figura abaixo). Sua massa é 60   k g . Despreze forças de atrito entre a balsa e a água, (a) A que distância da borda do píer está o centro de massa do sistema você-bal-sa? (b) Você caminha para a frente da balsa e para. A que distância da borda do píer o centro de massa está agora? (c) Quando você está na frente da balsa, a que distância você está da borda do píer?

Passo 1

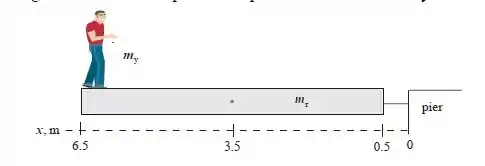
Deixando a origem na borda do píer e a direção +x para a direita, como mostrado na representação abaixo.

Passo 2

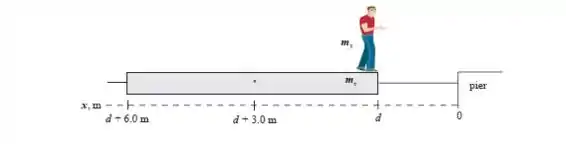
Na seguinte representação abaixo, d é a distância do final da balsa do cais depois de ter andado até a frente. A jangada se move para a esquerda enquanto você se move para a direita; com o centro de massa do sistema de jangada restante fixo (porque F e x t , r e s =   0 ). O diagrama mostra as posições inicial ( x y , i ) e final ( x y , i ) de si mesmo, bem como as posições inicial ( x r , c m , i   ) e final ( x r , c m , f   ) do centro de massa da jangada antes e depois de você ter caminhado para a frente da jangada.

Passo 3

Item (a)

x c m   antes de caminhar até a frente da jangada é dada por:

x c m = m y x y , i + m r x r , c m , i m y + m r

Substituindo por valores numéricos:

x c m = 60   k g 6,5   m + 120   k g 3,5   m 60 k g + 120   k g = 4,5   m

Passo 4

Item (b)

Como F e x t , r e s = 0 , o centro de massa permanece fixa:

x c m ' = x c m = 4,5   m

Passo 5

Item (c)

Chame a distância da jangada até o cais depois de ter caminhado para a frente da balsa d e expresse a nova localização x c m '     do centro de massa do sistema:

x ' c m = m y x y , f + m r x r , c m , f m y + m r = m y d + m r d + 3,0   m m y + m r = 4,5   m

Então, isolando a distância d :

d = 4,5   m m y + 1,5   m m r m y + m r

Substituindo por valores numéricos:

d = 4,5   m ( 60   k g ) + 1,5   m ( 129   k g ) 60   k g + 120   k g = 2,5   m

Resposta

a   x c m = 4,5   m

b   x c m ' = 4,5   m

c   d = 2,5   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Após uma colisão perfeitamente inelástica, dois objetos de mesma massa e mesma velocidade escalar inicial deslocam-se juntos com metade da velocidade inicial. Determine o ângulo entre as velocidades i
A bola B , que se move no sentido positivo de um eixo x com velocidade v , colide com a bola A inicialmente em repouso na origem. A e B têm massas diferentes. Após a colisão, B se move no sentido nega
Dois corpos de 2,0k g , A e B , sofrem uma colisão. As velocidades antes da colisão são v 1=( 15 i →+30 j → ) m / s e v 0=( - 10 i →+5,0 j → )m / s . Após a colisão, v , .=( - 5 ,0 i →+20j → )m / s .
Na Fig. 9-21, a partícula 1 é uma partícula alfa e a partícula 2 é um núcleo de oxigênio . A partícula alfa é espalhada de um ângulo θ 1=64,0 ° e o núcleo de oxigênio recua com uma velocidade escalar
Uma reação nuclear. A fissão, processo que fornece energia para um reator nuclear, ocorre quando um núcleo pesado é dividido em dois núcleos com pesos médios. Uma dessas reações ocorre quando um nêutr