Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 8.Problemas - Ex. 46

Um foguete tem massa total M i   =   360   k g , incluindo M f   =   330   k g de combustível e oxidante. No espaço interestelar, ele parte do repouso na posição x   =   0 , liga o motor no instante t   =   0 e expele gases de exaustão com velocidade relativa v e   =   1500   m / s à taxa constante k   =   2,50   k g / s . O combustível durará por um tempo de queima T b   =   M f   / k   =   330   k g / ( 2,5   k g / s )   =   132   s . (a) Mostre que durante a queima a velocidade do foguete em função do tempo é definida por v t =   - v e ln ⁡ (   1 - k t M i   ) (b) Faça um gráfico da velocidade do foguete em função do tempo para os instantes entre 0 e 132 s. (c) Mostre que a aceleração do foguete é a t = k v e M i - k t (d) Faça um gráfico da aceleração em função do tempo. (e) Mostre que a posição do foguete é x t = v e   M i k - t ln ⁡ 1 - k t M i + v e t (f) Faça um gráfico da posição durante a queima em função do tempo.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Da equação para propulsão de foguete:

v - 0 = v e ln ⁡ M i M f = - v e ln ⁡ M f M i

Agora, M f = M i - k t , então:

v = - v e ln ⁡ M i - k t M i = - v c ln ⁡ 1 - k M i t

Com a definição, T p ≡ M i k se torna:

v t = - v e ln ⁡ 1 - t T p

Passo 2

Letra b:

Com v e = 1500 m s ,   e  T p = 144 s , temos:

v = - 1500 m s ln ⁡ 1 - t 144 s

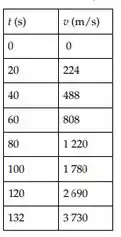
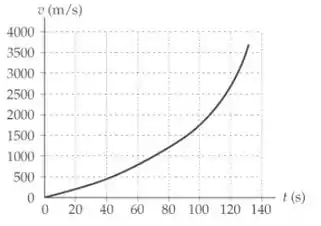
Passo 3

Letra c:

a t = d v d t = d - v e ln ⁡ 1 - t T P d t = - v e 1 1 - t T p - 1 T p = v e T p 1 1 - t T p

a t = v e T p - t

Passo 4

Letra d:

Com v e = 1500 m s ,   e   T p = 144 s , a = 1500 m s 144 s - t , temos:

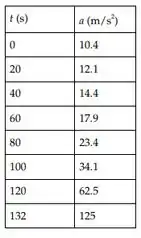
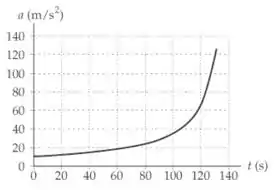
Passo 5

Letra e:

x t = 0 + ∫ 0 t   v d t = ∫ 0 t   - v e ln ⁡ 1 - t T p d t = v e T p ∫ 0 t   ln ⁡ 1 - t T p - d t T p

x t = v e T p 1 - t T p ln ⁡ 1 - t T p - 1 - t T p 0 t

x t = v e T p - t ln ⁡ 1 - t T p + v e t

Passo 6

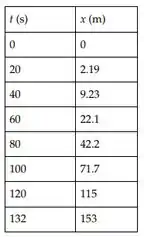
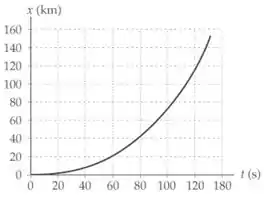
Letra f:

Com v e = 1.500 m s = 1.50 k m s ,   e   T p = 144 s , temos:

x = 1.50 144 - t ln ⁡ 1 - t 144 + 1.50 t

Resposta

  1. - v e ln ⁡ 1 - t T p
  2. V e r   g r á f i c o
  3. v e T p - t
  4. Ver gráfico
  5. v e T p - t ln ⁡ 1 - t T p + v e t
  6. Ver gráfico
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um astronauta de 70 kg flutuando no espaço no interior deuma UMM ( unidade de manobra manual ) sofre uma aceleração de 0,029 m/s quando ele aciona um dos motores de propulsãoa ) Sabendo que a velocida
Um modelo de motor de foguete C 6-5 possui um impulso igual a 10,0 Ns durante 1,70 s, enquanto queima 0,0125 kg de combustível. Sua força de propulsão máxima é igual a 13,3 N. A massa inicial do motor
Obviamente um foguete pode ser acelerado até atingir velocidades muito elevadas, porém, qual deve ser uma velocidade máxima razoável? Considere um foguete disparado a partir do repouso no espaço sider
Um foguete com estágio único é disparado a partir do repouso no espaço sideral, onde a gravidade é desprezível. Sabendo que ele queima seu combustível em 50,0 s e que a velocidade relativa do gás de e
Suponha que a massa do foguete descrito nos Exemplos 8.15 e 8.16 (Seção 8.6) seja uma função do tempo dada por m t = m 0        p a r at0 m 0 1 - t 120 s        p a r a0 ≤ t ≤ 90 s m 0 / 4        p a