Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.Problemas Adicionais - Ex. 108
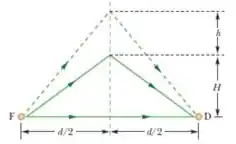
Uma fonte e um detector de ondas de rádio estão a uma distância em um terreno plano (veja a figura). Ondas de rádio de comprimento de onda chegam ao detector de duas formas: diretamente e depois de serem refletidas em certa camada da atmosfera que sobre gradualmente. Quando a camada está a uma altura , as ondas chegam em fase ao detector ; quando a camada atinge a altura , as ondas têm fases opostas. Expresse em termos de , e .
Passo 1
Fala galerinha bonita, tudo beleza? Vamos entender o princípio que está sendo discutido aqui.
Como as ondas percorrem distâncias diferentes dependendo do caminho tomado (direto ou indireto), quando chegarem em , elas podem ter fases diferentes, como nesse caso:
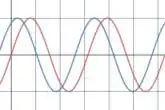
Mas o que o enunciado diz é que, quando elas tomam o caminho definido pela altura , elas chegam exatamente em fase (uma onda em cima da outra):
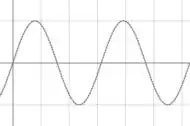
E quando tomam o caminho definido por , elas chegam em fases opostas:
Passo 2
Ok, já entendemos o que está acontecendo, agora vamos escrever isso matematicamente.
Quando as ondas estão em fase, isso quer dizer que a diferença de caminho entre elas é algum múltiplo de um comprimento de onda inteiro:
E quando estão em fases opostas, a diferença de caminho entre elas é algum múltiplo de meio comprimento de onda:
Vamos procurar expressões para cada uma das diferenças de caminho.
Passo 3
Começando pela diferença entre o caminho direto (de comprimento ) e o caminho definido pela altura
Onde nós usamos o teorema de pitágoras para calcular a distância do caminho indireto (dê uma olhada no desenho para entender isso melhor).
E podemos fazer a mesma coisa para a outra diferença de caminho:
Então ficamos com duas equações:
Se fizermos a segunda equação menos a primeira, vamos chegar no seguinte:
Nosso objetivo é escrever em função de , e , então agora é só isolar:
Resposta
O comprimento de onda é .