Duas fontes sonoras oscilam em fase com uma frequência de . Em um ponto a de uma das fontes e a da outro, a amplitude do som proveniente da cada fonte, em separado, é . (a) Qual é a diferença de fase entre as duas ondas nesse ponto (b) Qual é a amplitude (em termo de ) da onda resultante nesse ponto?
Passo 1
Antes de começarmos a brincadeira, vou te mostrar um conceito chamado fasores que deixa esse tipo de questão mamão com açúcar. Vem comigo!
A ideia é tratar ondas como vetores, onde o modulo do vetor será nossa amplitude e seu ângulo com o eixo será a fase.
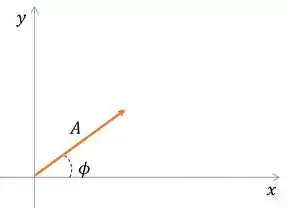
Passo 2
Primeiro vamos achar a diferença de fase entre as ondas.
Nosso será o seguinte:
Considerando a velocidade do som como :
Fazendo as contas:
Agora vem a parte mais legal. Quando formos sobrepor as ondas, bastar somarmos vetores 😉. Então vamos ver como vai ficar!
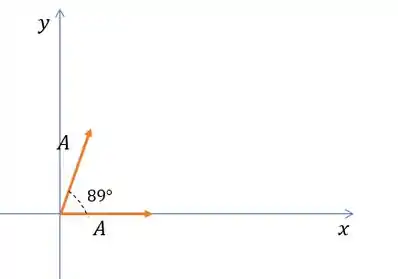
Duas ondas de amplitudes iguais e defasadas de . Quando usarmos fasores, fazemos dois vetores de módulos iguais as amplitudes e o ângulo entre eles de
Passo 3
Agora é só achar o modulo do vetor resultante que acharemos o amplitude da onda resultante.
Logo,
Portanto,