Um bloco de é preso a uma das extremidades de uma mola com uma constante elásstica de e forçado a oscilar por uma força , em que . A constante de amortecimento é . Em , o bloco está em repouso com a mola relaxada. (a) Use integração numérica para plotar o deslocamento do bloco durante o primeiro . Use o movimento perto do final do intervalo de para estimar a amplitude, o período e a frequência angular. Repita os cálculos para (b) e (c) .
Passo 1
Primeiro precisamos encontrar uma equação diferencial que descreva o movimento do oscilador.
Para isso vamos usar a segunda lei de Newton:
Onde é a segunda derivada temporal da coordenada :
Agora vamos reescrever cada um dos termos: lembrando de colocar os sinais negativos na força elástica e na força de amortecimento.
Passo 2
Agora vamos substituir os valores numéricos:
O enunciado pediu para resolvermos essa equação por integração numérica. Não é tão simples fazer integração numérica para uma equação diferencial de segunda ordem, então vamos com calma.
Passo 3
Inicialmente o que nós temos é uma equação diferencial de segunda ordem e duas condições iniciais:
Se você colocar essas informações em um programa de integração numérica, vai chegar em um gráfico como esse:
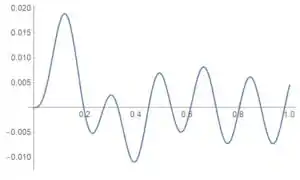
Mas vamos ver o que conseguimos fazer por conta própria (o computador será sempre indispensável).
Primeiro nós vamos converter aquela equação diferencial de segunda ordem em duas equações de primeira ordem, fazendo a seguinte substituição:
Então ficamos com um par de duas equações de primeira ordem, cada uma com sua própria condição inicial.
Passo 4
Agora vamos separar o intervalo do eixo em vários pedaços. O enunciado pediu para plotarmos entre e , então vamos pegar pedaços de cada, compreendendo esse intervalo inteiro:
E então vamos transformar cada uma daquelas equações diferenciais em equações que dêem um valor para cada passo . Começando pela primeira equação:
Vamos aproximar e . Então:
E agora vamos fazer o mesmo para a segunda equação:
Usando as mesmas aproximações de antes, ficamos com o seguinte:
Agora podemos usar um programa de planilhas para repetir esses passos várias vezes. Para cada valor de fazemos os cálculos de forma a preencher a seguinte tabela com as seguinte fórmulas:

Passo 5
(a) Quando montamos essa tabela em um programa de planilhas e repetimos até (o que acontece quando ), ficamos com um gráfico de em função de idêntico ao que colocamos lá no segundo passo.
E o nosso objetivo é estimar o período, a amplitude e a frequência angular olhando para os valores no final do gráfico.
Você pode pedir para o seu programa de planilhas fazer o gráfico apenas em , e então ficará com algo assim:
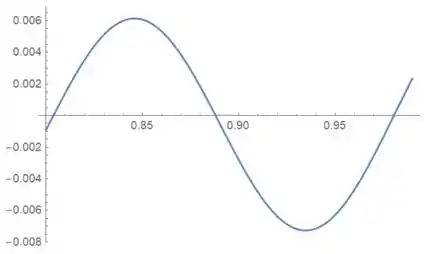
Daqui podemos obter as estimativas que foram pedidas:
Onde é a amplitude da curva.
Passo 6
(b) Agora vamos fazer o mesmo para o caso em que , ou seja:
Esse termo só aparece dentro do seno em , então só o que precisamos fazer é voltar nessa equação e trocar o valor.
A partir daí, construímos o mesmo gráfico de antes. Primeiro mostrando tudo até
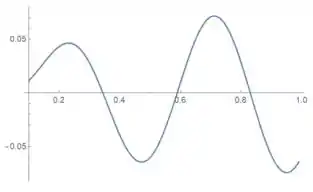
Aqui não é tão fácil estimar os valores, porque temos pouco mais de uma oscilação completa no primeiro segundo. Mas vamos tentar:
Passo 7
(c) Agora queremos fazer o mesmo, mas para o caso em que . Só precisamos fazer a troca no mesmo termo de antes, e ficaremos com o seguinte gráfico:
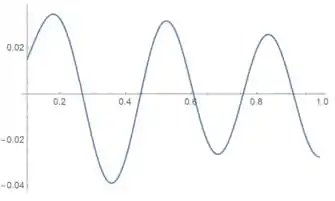
Dessa vez os valores estão um pouco mais fáceis de estimar:
Resposta
(a) , , .
(b) Para , temos: , , .
(c) Para , temos: , , .