Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 41
Uma fonte puntiforme de luz esta localizada a 5,0m abai-
xo da superficie de uma grande piscina de agua.Determine a area
do maior circulo na superficie da piscina atraves do qual a luz vinda
diretamente da fonte pode emergir.
Passo 1
Podemos aplicar a lei de Snell à interface água-ar para expressar o ângulo crítico em termos dos índices de refração da água e do ar e, a seguir, relacionar o raio do círculo à profundidade d da fonte pontual e .
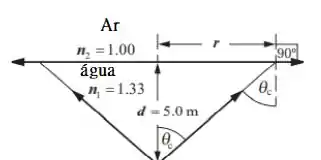
Passo 2
Expresse a área do círculo cujo raio é r:
Relacione o raio do círculo com a profundidade d do ponto de origem e o ângulo crítico
Aplique a lei de Snell à interface água-ar para obter:
Resposta
Exercícios de Livros Relacionados
Considere a experiência dos anéis de Newton, descrita na Seç. 3.3. Uma lente plano-convexa de raio de curvatura R é colocada em contato com uma plana de vidro e iluminada na incidência perpendicular (
Um dispositivo para a obtenção de anéis de Newton consiste em uma lente plano-convexa de vidro com raio de curvatura R que repousa sobre uma placa plana de vidro, como mostrado na Figura 33-42. O film
Considere que, antes que a lente do problema 32 seja colocada sobre a placa, um filme de óleo com índice de refração igual a 1,82 seja depositado sobre a placa. Quais seriam, então, os raios das prime
Uma lente de vidro plano-convexa de raio de curvatura 2,00m repousa sobre uma placa de vidro opticamente plana. O arranjo é iluminado de cima usando luz monocromática com comprimento de onda de 520n m
A lente de uma câmera é feita de vidro com índice de refração de 1,60. Esta lente é coberta com um filme de fluoreto de magnésio (índice de refração igual a 1,38) para aumentar a transmissão da luz. O