Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 85
A lente de uma câmera é feita de vidro com índice de refração de 1,60. Esta lente é coberta com um filme de fluoreto de magnésio (índice de refração igual a 1,38) para aumentar a transmissão da luz. O propósito deste filme é produzir uma reflexão nula para luz com comprimento de onda de 540 nm. Considere que a superfície da lente seja plana e que o filme tenha uma espessura uniforme e plana.
a) Qual é a espessura mínima deste filme para este objetivo?
b) Haveria interferência destrutiva para qualquer outro comprimento de onda na faixa do visível?
c) Por qual fator a reflexão da luz com comprimento de onda de 400 nm seria reduzida pela presença deste filme? Despreze a variação da amplitude da luz refletida pelas duas superfícies.
Passo 1
Meus queridos e minhas queridas!
Vamos por etapas. Pelo diagrama abaixo, percebemos que a luz refletida nas interfaces ar-filme e filme-lente há uma mudança de fase de . Podemos usar a condição de interferência destrutiva entre a luz refletida pela interface ar-filme e a filme-lente para encontrar a espessura do filme. Para responder a letra c) podemos encontrar o fator no qual a luz fornecida pelo comprimento de onda é reduzida pelo filme com .
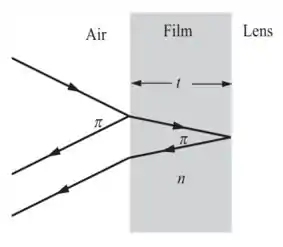
Sendo a condição de interferência destrutiva:
Ou seja:
Passo 2
No item a):
Para m = 0:
Aplicando os valores fornecidos pela questão:
Passo 3
No item b) vamos encontrar o comprimento de onda do ar para m = 1:
Isolando :
Aplicando os valores fornecidos:
Logo, a resposta da pergunta é NÃO, já que 180 nm não faz parte da porção visível do espectro.
Passo 4
Por fim, no item c) vamos representar o fator de redução f como uma função da diferença de fase entre duas ondas refletidas:
Ok, agora vamos relacionar a diferença de fase com a diferença de caminho:
Sendo: .
Substituindo a relação encontrada na equação inicial:
Onde:
Aplicando:
Substituindo pelos valores fornecidos na questão: