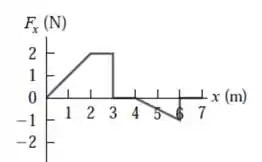
Uma força é aplicada paralelamente ao eixo O x a um modelo de carro de 2,0k g com controle remoto. O componente x da força varia com a coordenada x do carro conforme indicado na Figura 6.32 . Calcule o trabalho realizado pela força quando o carro se desloca a) d ex = 0ax = 3,0m ; b) d ex = 3ax = 4,0m ; c) d ex = 4ax = 7,0m d) d ex = 0ax = 7,0m ; e)d ex = 7,0max = 2,0m .

a ) 4 J b ) 0 J c ) - 1 J d ) 3 J e ) - 1 J

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.3 - Ex. 37

Uma força é aplicada paralelamente ao eixo a um modelo de carro de com controle remoto. O componente da força varia com a coordenada do carro conforme indicado na Figura . Calcule o trabalho realizado pela força quando o carro se desloca

a)

b) ;

c)

d)

e)

Passo 1

Opa, bora lá! Esse enunciado tem uma historinha mas o que importa é esse gráfico aqui:

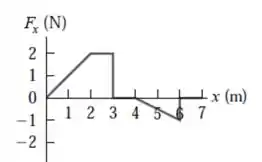
Temos que calcular o trabalho de deslocamento em diferentes trechos!

O trabalho de uma força variável pode ser calculado de duas maneiras: ou integrando a força por todo deslocamento (daí você vai precisar da expressão matemática da força) ou pela área do gráfico no intervalo do deslocamento que você quer (que é esse nosso caso aqui!).

Nota que podemos calcular a área embaixo dessa curva de força aí do desenho, é só fatiar essa área em formas geométricas que conhecemos como, por exemplo, retângulos e triângulos. Beleza?

Ah! Aqui temos um detalhe: a área que estiver abaixo do eixo horizontal vai ser negativo, ok?

Passo 2

De temos que essa área pode ser dada pela soma de um retângulo de base e altura mais a área de um triângulo de base e altura também . Agora é só calcular a soma das áreas:

Passo 3

O trabalho de vai ser nulo, pois a força é nula nesse deslocamento.

Passo 4

O trabalho de vai ser dividido em um triângulo de base e altura e uma parte de trabalho nulo, entre . Assim o trabalho vai ser só a área do triângulo:

Passo 5

O trabalho total de pode ser calculado a partir da soma dos trabalhos separadamente. Então juntando os resultados dos itens anteriores temos:

Passo 6

Por fim o exercício pede para calcularmos o trabalho de . Aqui temos que tomar um cuidado. O deslocamento vai ser oposto à direção da força, então o sinal do trabalho que encontrarmos será trocado.

De e de o trabalho é nulo.

De já calculamos o trabalho e ele deu , mas como estamos indo na direção oposta o trabalho de vai ser .

Por fim de é igual ao trabalho de , um retângulo de base que calculamos na letra , e esse trabalho vale , como estamos indo na direção oposta, então o trabalho que queremos de .

O trabalho total vai ser a soma dos trabalhos:

Prontinho!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força orientada no sentido positivo do eixo +Ox possui módulo F = b/xn, onde b e n são constantes. a) Para n1, calcule o trabalho realizado por essa força sobre uma partícula que se move ao longo

Um bloco de gelo de 4,0k g é colocado contra uma mola horizontal cuja constante da força é k = 200N / m , sendo comprimida em 0,025m . A mola é liberada e acelera o bloco em uma superfície horizontal.

Suponha que o modelo de carro do Exercício 6.37 esteja inicialmente em repouso em x = 0 e que seja a força resultante atuando sobre o carro. Use o teorema do trabalho-energia para calcular a velocidad

Uma força de 160N estica 0,050m uma certa mola a partir do seu comprimento sem deformação. a) Qual é a força necessária para esticar essa mola 0,015m a partir do seu comprimento sem deformação? E para

Uma vaca está saindo do celeiro, apesar de você tentar puxá-la de volta. Nas coordenadas com origem na porta do celeiro, a vaca caminha de x =0 até x = 6,9m enquanto você aplica uma força com o compon