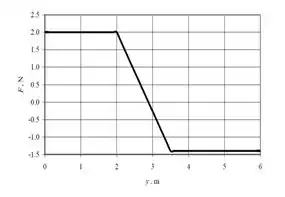
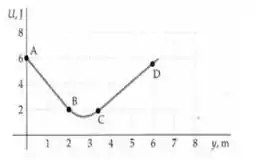
26. A força é associada à função energia potencial . Na curva de energia potencial , mostrada na figura abaixo, os segmentos e são linhas retas. Faça o gráfico de . Coloque valores numéricos, com unidades, nos dois eixos. Estes valores podem ser obtidos no gráfico de .
Passo 1
, de exercícios anteriores, é definido como o negativo da derivada do valor função de energia potencial em relação a ; isto é, . Consequentemente, de acordo com a prória definição da derivada, a qual fornece justamente a taxa de variação; podemos obter examinando as inclinações do gráfico de em função de .
Para isso, iremos analisar os três intervalos expostos no gráfico do enunciado: e
Temos que para a taxa de variação no intervalo , dado que é uma reta; basta calcular o coeficente angular do triângulo formado:
Temos que a taxa de variação no intervalo , dado que é uma curva, irá variar ao longo da curva. Mas sabe-se basicamente que irá transitar de até , na forma de uma reta, uma vez que analisando a curva , vemos que assemelha-se a uma função do segundo grau, cuja primeira derivada é justamente a função de grau anterior, ou seja, justamente uma reta.
Temos que para a taxa de variação no intervalo , dado que é uma reta; como não se sabe ao certo em que pontos o segmento de reta está tocando, estimam-se os valores de , para os pontos e de modo a ser possível calcular o coeficiente angular do triângulo formado. Logo:
Passo 2
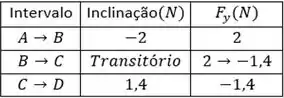
Com base nos dados anteriores, monta-se então a seguinte tabela para auxiliar na construção do gráfico. Vale lembrar que , ou seja o produto da inclinação por :
Passo 3
Por último, com os valores obtidos anteriormente, finalmente podemos traçar o gráfico de em função de , que começa na origem e vai ter a seguinte cara:
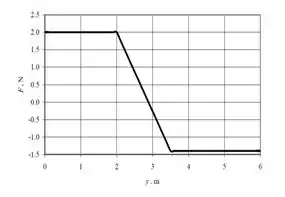
Resposta