Dois blocos, de massas e escorregam para baixo sobre um plano inclinado, como mostrado na figura abaixo. Eles estão ligados por um bastão sem massa. Os coeficientes de atrito cinético entre o bloco e a superfície são , para o bloco 1 e para o bloco 2. (a) Determine a aceleração dos dois blocos. (b) Determine a força que o bastão exerce sobre cada um dos dois blocos. Mostre que estas forças são ambas nulas quando e dê um argumento não-matemático simples para que isto seja verdadeiro.

Passo 1
Letra (a)
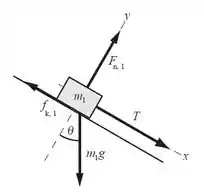
Os dois blocos vão descer com a mesma aceleração (por causa do fio). O que a gente vai fazer é usar a segunda lei de Newton quatro vezes: em x e em y, e em cada bloco. Vamos começar com o bloco 1:
e
Passo 2
Substitui (2) em (1):
Passo 3
Agora vamos fazer a mesma coisa, só que no bloco 2:
e
Passo 4
Substitui (5) em (4):
Passo 5
A gente ainda não quer a tração (isso fica para a letra b), só a aceleração. Então podemos sumir com a tração T somando (3) com (6):
Agora isola o :
Passo 6
Letra (b)
Para a gente conseguir o T, a gente pega a equação (3), divide ela por e obtém a equação (7). Depois pega a equação (6), divide ela por e obtém a equação (8). Por fim a gente faz (7) – (8), que o some:
Agora com (6)
Passo 7
(7) – (8):
Passo 8
Se , a tensão T vai pra 0 (olha a equação (9)). Outra forma de concluir isso é perceber que, se eles têm o mesmo coeficiente de atrito, os blocos descem com a mesma aceleração, então o fio não comprime nem estica, e aí fica com tensão 0.
Resposta
Letra (a):
Letra (b): ver solução.