Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 32
32. Uma força é dada por , onde .
(a) Para valores positivos de , a energia potencial associada a essa força aumenta ou diminui com o aumento de ? (Você pode encotrar a resposta para esta questão imaginando o que acontece com uma partícula que é colocada em repouso em algum ponto e depois largada.) (b) Encontre a função de energia potencial associada a essa força de modo que tende a zero e tende ao infinito.
(c) Esboçe versus .
Passo 1
(a)
Já tá até ficando chato resolver esse tipo de questão, de tão repetitivo que tá, mas vamos lá!
A força, , é definida como o negativo da derivada da função de energia potencial em relação a , ou seja, . Consequentemente, como queremos trabalhar com a energia potencial associada, basta integral em relação a , para encontrar
Ou seja:
A integral indefinida já deu direto a energia inicial , que nada mais é do que a constante de integração.
e , pela fórmula acima, são inversamente proporcionais. Logo, a medida que aumenta, diminui.
Passo 2
(b) Na letra (a) obtivemos a seguinte fórmula para a energia potencial:
Agora vamos analisar com um pouco mais de cuidado essa fórmula.
Temos que está no denominador da expressão acima. Logo, podemos estabelecer a seguinte relação, se tender ao infinito:
Uma vez que , então . Ou seja conforme vai pro infinito, vai pra zero.
A questão também diz que deve tender apenas para zero. Logo, nosso amiguinho também vai ser zero, de modo que resta a expressão final correspondente:
Passo 3
(c) Bom! Só nos resta então traçar o gráfico para a função abaixo:
Acho que todo mundo já tá careca de saber como ficará esse gráfico. Isso mesmo! Ele tem um formato de hipérbole. Mas atenção, que só queremos os valores positivos de .
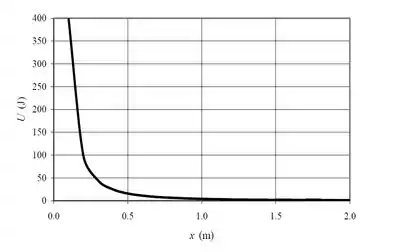
Ta aí!
Resposta
a) A energia potencial diminui
b)
c) Resolução Gráfica