Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 25
25. A força é associada à função energia potencial , onde é uma constante positiva.
(a) Determine a força como função de .
(b) Essa força está apontando para a origem ou para longe dela, na região ? Repita a pergunta para a região.
(c) A energia potencial aumenta ou diminui quando cresce na região?
(d) Responda às Partes (b) e (c) com a constante negativa.
Passo 1
a) Olá, querido? Cê tá bem? Então, ele deu a função da energia potencial:
E pede a força em função de . Ou seja, ele quer a função força .
Para achar uma função força a partir de uma função potencial a gente pode usar a relação:
Sendo que . Substituindo:
Então basicamente a gente precisa derivar e mudar o sinal para achar . Vamos calcular essa derivada:
Usando a regrinha de derivar polinômios:
Passo 2
b) Cara, se uma partícula está numa posição positiva e a força sobre ela aponta para a origem, quer dizer que a força aponta para esquerda, ou seja, que a força tem valor negativo:
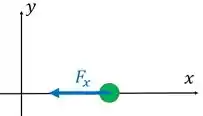
E se ela aponta para longe da origem, ela é positiva. Então o que a gente precisa ver é se , a força é positiva ou negativa. Nossa expressão da força é:
é sempre um valor positivo, independente de . Como a constante é sempre positiva, então é sempre positiva independentemente de .
Logo, em , a força aponta para longe da origem.
Agora se a partícula estiver em , e a força for positiva, ela aponta para a origem:
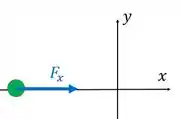
Então como a nossa força é sempre positiva, quando a partícula estiver em , ela vai apontar para a origem.
Passo 3
c) Para responder a esse item, basta dar uma olhada na estrutura da fórmula que descreve a energia potencial:
Os termos e são inversamente proporcionais e como , logo pode-se afirmar com exatidão, que diminui com o crescimento de na região positiva.
Já que se , que é o denominador, fica sendo um valor cada vez maior e sempre positivo, fica cada vez menor.
Passo 4
d) Esse item é justamente o inverso das letras b e c. Ou seja, se a constante for negativa, a força será sempre negativa e apontada no sentido negativo do eixo (para a esquerda), independentemente se a partícula estiver em ou .
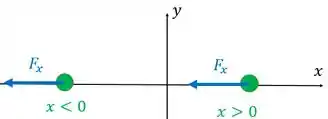
Logo na região , a força está direcionada para longe da origem e na região , ela está direcionada para perto da origem.
Em relação à energia potencial na região , uma vez que a constante agora é negativa, podemos dizer que irá aumentar com o crescimento de na região positiva.
Porque se , e , é um valor negativo. E assim, se aumenta, fica sendo um valor em módulo menor. Mas como ele é negativo, ele se torna um valor maior ao diminuir em módulo.
Assim como é um valor maior que . é menor em módulo que , mas como eles são negativos, o valor com módulo menor será maior.
Resposta
a)
b) Na região , a força está apontando para longe da origem e na região , a força está apontando para perto da origem.
c) diminui com o crescimento de na região .
d) Na região , a força está apontando para longe da origem e na região , a força está apontando para perto da origem. aumenta com o crescimento de na região .