Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 30
30. A força resultante que atua sobre um corpo restringido ao eixo é dada por . (A força está em newtons e em metros.) Localize as posições de equilíbrio instável e estável. Mostre que cada posição é estável ou instável, calculando a força de um milímetro em cada lado das posições.
Passo 1
As posições de equilíbrio são aqueles valores de para os quais . Se as posições de equilíbrio são estáveis ou instáveis, depende dos sinais da força em ambos os lados da posição de equilíbrio. Basicamente, o objetivo vai ser encontrar os valores referentes às posições de equilíbrio e com estas posições, substituir o antecessor e o sucessor em um milímetro na equação que descreve a força. Se os sinais obtidos forem os mesmos, então o equilíbrio é instável. Mas se os sinais forem diferentes, o equilíbrio será estável !
Passo 2
Começa-se então, igualando a força a zero, a fim de encontrar as posições de equilíbrio:
Passo 3
c) Observando que precisamos apenas determinar se cada valor de é positivo ou negativo, avalia-se nas seguintes posições: em e para determinar o equilíbrio em … e em seguida repete-se esses cálculos em ,
e, para determinar a estabilidade em e , respectivamente:
Para
Para
Para
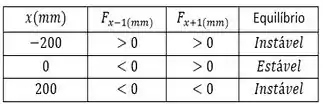
Resposta
.